Nagel Point and Centroid on Adjacent Isosceles Triangles
Source
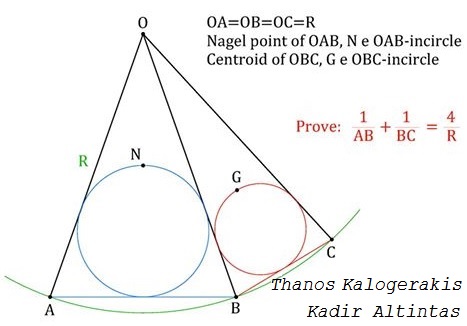
Problem

Solution 1
Let $OB=x+y,\,$ $OC=x+z,\,$ $BC=x+y.\,$ We've shown elsewhere that $(x+y+z)^2=4(xy+yz+zx).\,$ WLOG, $x+yz=6.\,$ Since $OB=OC,\,$ $z=y,\,$ so that
$\left\{\begin{align}x+2y=6\\y^2+2xy=9\end{align}\right. ,$
with two solutions: $(x,y)=(0,3)\,$ $(x,y)=(4,1).\,$ $x=0\,$ does not make sense, thus $OB=OC=5=R\,$ and $BC=2.$
We now pass to $\Delta AOB.\,$ Let $AB=2u\lt 10.\,$ We have the semiperimeter $p=5+u\,$ and $p-OA=p-OB=u.\,$ Let $D\,$ be the midpoint, $I\,$ the incenter, of $\Delta AOB.\,$ Then $\displaystyle \overset{\rightarrow}{OI}=\frac{\overset{\rightarrow}{OA}+\overset{\rightarrow}{OB}}{2},\,$ $\displaystyle \overset{\rightarrow}{ON}=\frac{u(\overset{\rightarrow}{OA}+\overset{\rightarrow}{OB})}{5+u}\,$ and $\displaystyle \overset{\rightarrow}{OD}=\frac{\overset{\rightarrow}{OA}+\overset{\rightarrow}{OB}}{2}.\,$ It follows that $\displaystyle \frac{5u}{5+u}=\frac{1}{2},\,$ i.e., $\displaystyle u=\frac{5}{3},\,$ $\displaystyle AB=\frac{10}{3}\,$ such that, finally,
$\displaystyle \frac{1}{AB}+\frac{1}{BC}=\frac{3}{10}+\frac{1}{2}=\frac{4}{5}=\frac{4}{R},$
as required.
Solution 2

Solution 3
We know that $\displaystyle \frac{OB}{AB}=\frac{3}{2}\,$ and also that $\displaystyle \frac{OB}{BC}=\frac{5}{2}.\,$ Since, $OB=R,\,$ it follows that
$\displaystyle \frac{R}{AB}+\frac{R}{BC}=\frac{3}{2}+\frac{5}{2}=4,$
implying the claim.
Acknowledgment
The above problem - by Kadir Altintas and Thanos Kalogerakis - has been posted by Thanos Kalogerakis at the Peru Geometrico facebook group. Solution 1 is by Leo Giugiuc; Solution 2 is by Francisco Javier García Capitán; Solution 3 is by Thanos Kalogerakis and, independently, yours truly.
![]()
|Contact| |Up| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73571509
