ABC is an isosceles triangle with vertex angle BAC = 20° and AB = AC. Point E is on AB such that AE = BC. Find the measure of AEC.

Solution

Copyright © 1996-2008 Alexander Bogomolny

This solution has been reported in [Leikin"].

The proof is practically by construction.

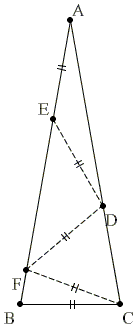
Starting from BC, form a sequence of isosceles triangles, BCF, CFD, FDE, DEA. Is it possible? Let us check the angles.

For ΔBCF to be isosceles, suffice it to pick BCF = 20°, for then BFC = 80° = CBF.

If point D on AC is such that DF = FC (and such point exists!), then, since DCF = 60°, ΔCDF is equilateral, with all the angles 60° and sides equal.

If E' on AB (not shown) is such that DF = DE' (and such a point exists), then ΔFDE' is isosceles, DFE' = 40° = FE'D and FDE' = 100°.

It follows that ADE' = 20° = AE'D. Therefore, ΔADE' is isosceles and DE' = AE'. But, by construction, DE' = DF = CF = BC. So, indeed, E = E'.

Since ΔCFD is equilateral, CD = BC = DE, so that ΔCDE is also equilateral with CDE = 100° + 60° = 160° which makes CED = 10°. Now, AEC = 140° + 10° = 150°.

Reference

1. R. Leikin, Dividable Triangles — What Are They?, Mathematics Teacher, May 2001, pp. 392–398.

Copyright © 1996-2008 Alexander Bogomolny