Twins Beget Twins
On November 12, 2011, Quang Tuan Bui reported a pair of Archimedean twins. On September 23, 2014, Floor van Lamoen published his discovery of another pair based on elaboration of Quang Tuan Bui's construction.
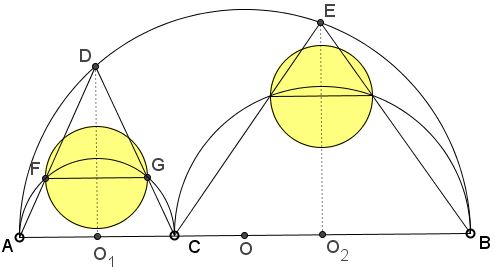
Consider an arbelos with $(O)$ being the semicircle with diameter $AB,$ while the point $C$ on $AB$ defines the smaller semicircles $(O_{1})$ and $(O_{2})$ on $AC$ and $BC,$ respectively. Let the perpendiculars to $AB$ from $O_{1}$ and $O_{2}$ meet $(O)$ in $D$ and $E,$ respectively. The segments $DA$ and $DC$ meet $(O_{1})$ in two points $F$ and $G.$ The segment $FG$ is the diameter of an Archimedean circle. Likewise an Archimedean circle is found from $E.$
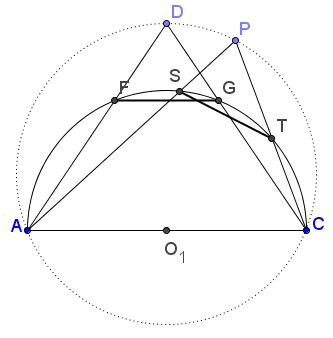
This is Quang Tuan Bui's construction. With this at hand, Floor van Lamoen asked what is the locus of points $P$ such that $PA$ and $PC$ cut a chord $ST$ off $(O_{1})$ congruent to $FG.$ To have $ST=FG$ it is necessary that the arcs subtended by these chords be equal, making angles $ADC$ and $APC$ also equal such that the quadrilateral $ADPC$ needs to be cyclic.
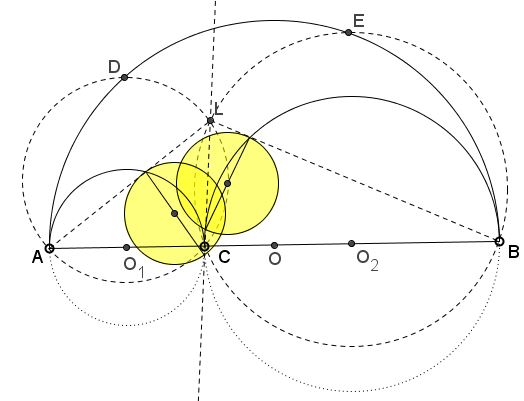
Thus it requires $P$ to lie on the circumcircle $(ACD)$ of $\Delta ACD.$ Similarly, the locus of $P$ such that $PB$ and $PC$ cut off $(O_{2})$ a chord congruent to the one cut off by $EB$ and $EC$ is the circumcircle $BCE.$ Now the circumcircles of $ACD$ and $BCE$ intersect, apart from $C,$ in a point $L.$ The point is remarkable in that $AL,CL$ and $CL,BL$ cut off $(O_{1})$ and $(O_{2}),$ respectively, congruent chords with diameters equal to that of the Archimedean twins!
- Arbelos - the Shoemaker's Knife
- 7 = 2 + 5 Sangaku
- Another Pair of Twins in Arbelos
- Archimedes' Quadruplets
- Archimedes' Twin Circles and a Brother
- Book of Lemmas: Proposition 5
- Book of Lemmas: Proposition 6
- Chain of Inscribed Circles
- Concurrency in Arbelos
- Concyclic Points in Arbelos
- Ellipse in Arbelos
- Gothic Arc
- Pappus Sangaku
- Rectangle in Arbelos
- Squares in Arbelos
- The Area of Arbelos
- Twin Segments in Arbelos
- Two Arbelos, Two Chains
- A Newly Born Pair of Siblings to Archimedes' Twins
- Concurrence in Arbelos
- Arbelos' Morsels
|Activities| |Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73581925
