Properties of Circle Through the Incenter

Circle through two vertices and the incenter of a triangle has many attractive properties.

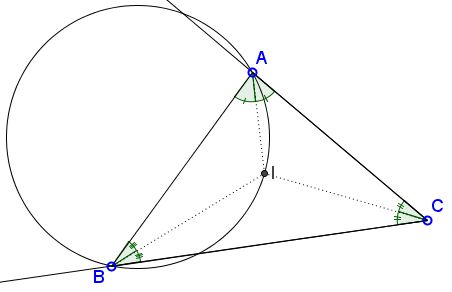
circle through the incenter - configuration

Below I list a few (that I know of) with proofs or links to the pages that establish these properties. Every one's welcome to suggest either properties not listed here or alternative proofs to the one that are.

The center of $(ABI)$ lies on the bisector of $\angle ACB.$

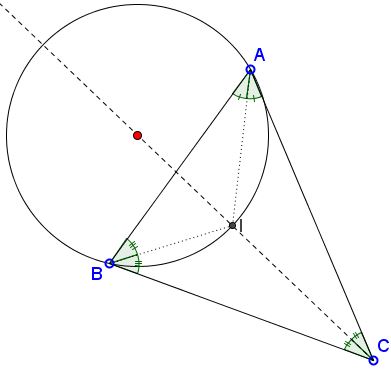
circle through the incenter has center on the opposite angle bisector

Proof

Let $X$ be the second intersection of $BC$ with $(ABI),$ $Y$ the second intersection of $AC$ with $(ABI).$

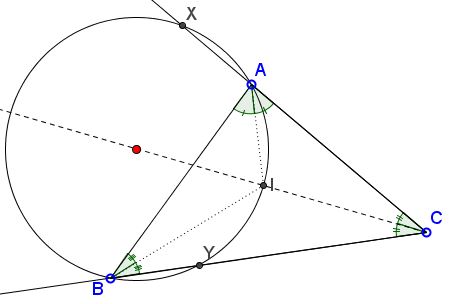
circle through the incenter cuts equal segments on two sides of the triangle

Then $AX=BY.$

Proof

Point $E$ on circle $(ABI)$ through $A,B,I$ has the property that $BE=AB.$

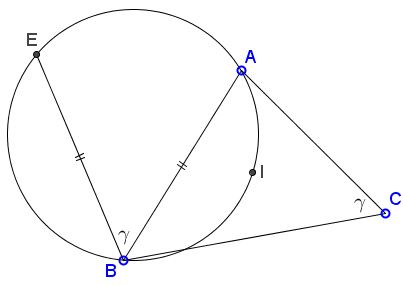
circle through the incenter - problem

Then $\angle ABE=\angle ACB.$

Proof

The center $O_c$ of $(ABI)$ lies on the circumcircle $(ABC).$

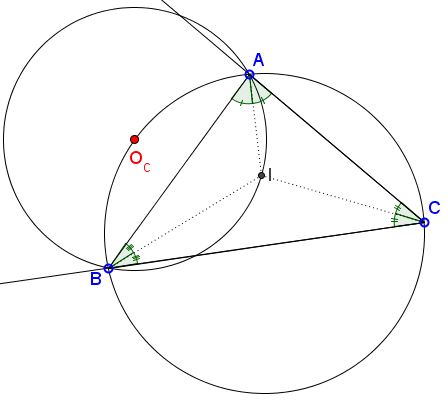
center of the circle through the incenter sits on the circumcircle of the triangle

Proof

Let $BE$ be a chord in $(ABI)$ such that $BE=AB.$ Let $O$ be the circumcenter of $\Delta ABC.$

a chord in (ABI) tangent to (ABC)

Then $BE\perp BO.$

Proof

72202085