Simple Property of Circle Through the Incenter
Problem
$I$ is the incenter of $\Delta ABC;$ point $E$ on circle $(ABI)$ thourgh $A,B,I$ has the property that $BE=AB.$
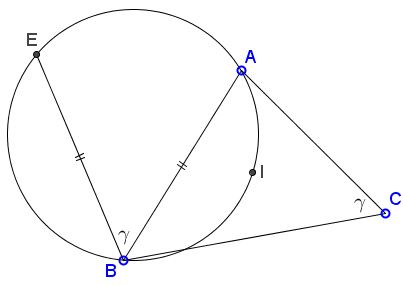
Prove that $\angle ABE=\angle ACB.$
Solution
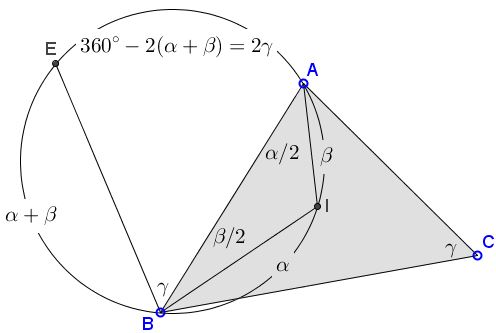
All one needs is a little "angle chasing" the details of which should be clear from the diagram below (just remember that the incenter lies at the intersection of the angle bisectors of the triangle.:
Acknowledgment
The problem was posted by Dao Thanh Oai at the at the CutTheKnotMath facebook page.
Note that circles through two vertices and the incenter of a triangle have other interesting properties.
|Contact| |Front page| |Contents| |Geometry| |Up|
Copyright © 1996-2018 Alexander Bogomolny73579676
