A Property of Circle Through the Incenter
Problem
$I$ is the incenter of $\Delta ABC.$
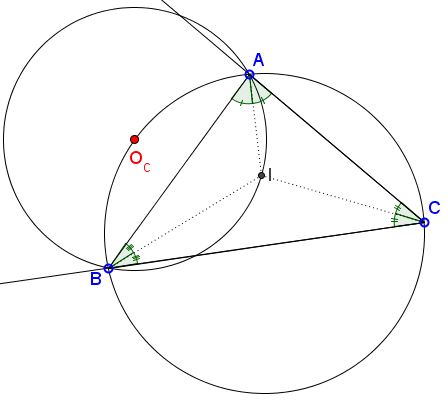
Prove that the center $O_c$ of $(ABI)$ lies on the circumcircle $(ABC).$
Proof
The proof follows by angle chasing. (The angles are as shown in the diagram.)
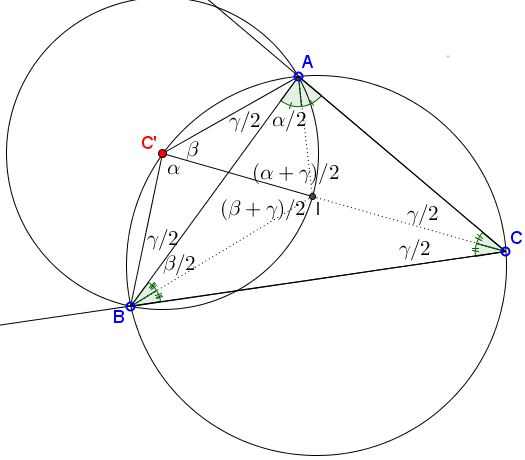
Let $C'$ be the intersection of the circumcircle $(ABC)$ with the bisector $CI$ of angle $ACB.$ Then $\angle ABC'=\angle BAC'=\gamma/2.$ Also, $\angle BC'C=\angle BAC=\alpha$ and $\angle AC'C=\angle ABC=\beta.$ It follows that $\angle C'AI=(\alpha+\gamma)/2$ and $\angle C'BI=(\beta+\gamma)/2.$ From here, $\angle AIC'=(\alpha+\gamma)/2=\angle C'AI$ and $\angle BIC'=(\angle (\beta+\gamma)/2=\angle C'BI,$ making triangles $AC'I$ and $BC'I$ isosceles: $AC'=IC'$ and $BC'=IC',$ implyig that $C'=O_c,$ the center of $(ABI).$
Acknowledgment
The problem was posted by Dao Thanh Oai at the at the CutTheKnotMath facebook page. Under a slightly different guise the problem was treated elsewhere at the site.
|Contact| |Front page| |Contents| |Geometry| |Up|
Copyright © 1996-2018 Alexander Bogomolny73579243
