Another Property of Circle Through the Incenter

$I$ is the incenter of $\Delta ABC.$ Let $BE$ be a chord in $(ABI)$ such that $BE=AB.$ Let $O$ be the circumcenter of $\Delta ABC.$

circle through the incenter and a tangent

Then $BE\perp BO.$

The proof follows by angle chasing. (The angles are as shown in the diagram.)

Let $O_c$ be t he center of $(ABI),$ $BG$ its diameter, and $BH$ a diameter of $(ABC).$

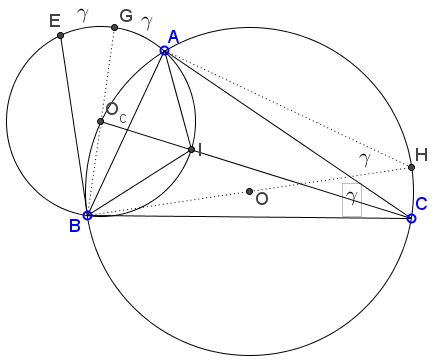
a reflection of a side in the diameter of the circle through the incenter

We know that

$\angle GBA=\angle O_{c}BA=\gamma/2.$
$BE$ is a reflection of $AB$ in the line $BO_c,$ i.e., $BG,$ implying that $\angle ABE=\gamma.$
$\angle AHB=\angle ACB=\gamma$ so that $\angle ABO=90^{\circ}-\gamma.$

It follows that $\angle EBO=\angle EBA+\angle ABO=\gamma+(90^{\circ}-\gamma)=90^{\circ}.$

The problem stemmed from the one posted by Dao Thanh Oai at the at the CutTheKnotMath facebook page.

71925124