A Property of Orthic Triangle
What is this about?
Problem
Let $H_{a}H_{b}H_{c}$ be the orthic triangle of $\Delta ABC;$ $AA'\perp H_{b}H_{c},$ $BB'\perp H_{a}H_{c},$ $CC'\perp H_{a}H_{b},$ as shown.
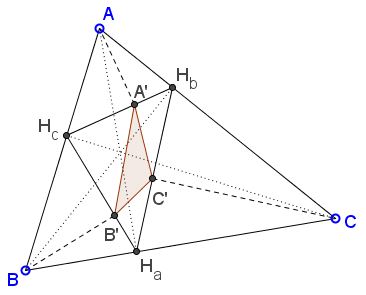
Let $[X]$ denote the area of shape $X.$ Prove that $[\Delta H_{a}H_{b}H_{c}]^{2}=[\Delta A'B'C']\cdot [\Delta ABC].$
Proof 1
It so happens that the lines $AA',$ $BB',$ $CC',$ when extended meet in the circumcenter $O$ of $\Delta ABC.$ (For a more astute person, this might be obvious I needed to play with GeoGebra to "discover" the fact.)
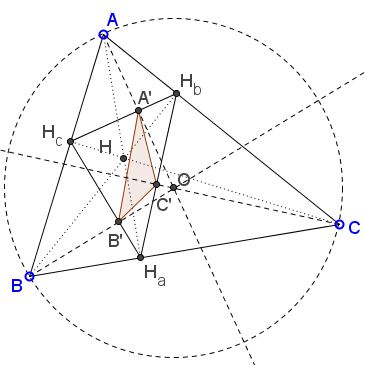
Why this is so? The altitudes in a triangle are perpendicular to the sides and so to all lines parallel to the sides. The lines joining the circumcenter with the vertices are perpendicular to the antiparallels and, therefore, to the sides of the orthic triangle, in particular. (This is because the orthocenter $H$ and the circumcenter $O$ are isogonal conjugate of each other.) It follows that $A'B'C'$ is the pedal triangle of $O$ with respect to $\Delta H_{a}H_{b}H_{c}.$
Now, there is a formula for the area of the pedal triangle in terms of elements of the base triangle, viz., for the pedal $\Delta DEF$ of point $P$ we have
$[\Delta EDF] = \displaystyle\frac{1}{4}(R^{2}-OP^{2})\cdot \frac{[\Delta ABC]}{R^{2}},$
where $R$ is the circumradius, $O$ the circumcenter of $\Delta ABC.$ We, thus, immediately have
$[\Delta H_{a}H_{b}H_{c}] = \displaystyle\bigg(\frac{R^{2}-OH^{2}}{4R^{2}}\bigg)\cdot [\Delta ABC],$
Concerning $\Delta H_{a}H_{b}H_{c}]$ we note that its circumcircle is the 9-point circle of $\Delta ABC,$ its center $N$ is half way between $H$ and $O$ ($ON=OH/2)$ and its circumradius is $R/2.$ It follows that
$\begin{align} [\Delta A'B'C'] &= \displaystyle\frac{(R/2)^{2}-(OH/2)^{2}}{4(R/2)^{2}}\cdot [\Delta H_{a}H_{b}H_{c}]\\ &= \displaystyle\bigg(\frac{R^{2}-OH^{2}}{4R^{2}}\bigg)\cdot [\Delta H_{a}H_{b}H_{c}] \\ &= \displaystyle\bigg(\frac{R^{2}-OH^{2}}{4R^{2}}\bigg)^{2}\cdot [\Delta ABC]. \end{align}$
The result follows.
Proof 2
We know that $[\Delta ABC]=2R^2\sin\angle A\sin\angle B\sin\angle C$ , where $R$ is the circumradius of $\Delta ABC.$ We also know that the angles of $\Delta H_a H_b H_c$ are $\pi-2A,$ $\pi-2B ,$ $\pi-2C$ and its circumradius is $R/2.$ It then follows that
$[\Delta H_a H_b H_c]=\frac{R^2}{2}\sin 2A\sin 2B\sin 2C.$
In $\Delta AH_b H_c,$ $A' H_b/A' H_c=\tan C/\tan B$ (because $AA'$ is an altitude). Similarly, we find $B' H_c/B' H_a=\tan A/\tan C$ and $C' H_a/C' H_b=\tan B/\tan A.$ By the inverse of Ceva's theorem, $A'B'C'$ is cevian relative to $\Delta H_aH_b H_c.$ Now we use the formula for area of cevian triangle to find that that
$\begin{align}\displaystyle [\Delta A' B' C' ] &= \frac{2\tan A\tan B\tan C}{(\tan A+\tan B)(\tan B+\tan C)(\tan C+\tan A)}\cdot [\Delta H_a H_b H_c ]\\ &= \frac{\displaystyle2\frac{\sin A}{\cos A}\frac{\sin B}{\cos B}\frac{\sin C}{\cos C}}{\displaystyle\frac{\sin C}{\cos A\cos B}\frac{\sin A}{\cos B\cos C}\frac{\sin B}{\cos C\cos A}}\cdot [\Delta H_a H_b H_c ]\\ &= 2\cos A\cos B\cos C \cdot [\Delta H_a H_b H_c ]. \end{align}$
In conclusion,
$\begin{align}\displaystyle [\Delta A' B' C' ]\cdot [\Delta ABC]&=(4R^2 \sin A\sin B\sin C )(\cos A\cos B\cos C\cdot [\Delta H_a H_b H_c ])\\ &= \frac{R^2}{2}\sin 2A\sin 2B\sin 2C\cdot [\Delta H_a H_b H_c ]\\ &=[\Delta H_a H_b H_c ]^2. \end{align}$
Acknowledgment
The problem has been posted by Bùi Quang Tuán at the CutTheKnotMath face book page with a link to his post at the Advanced Plane Geometry Yahoo group, where Nikolaos Dergiades supplied the same proof earlier and apparently with no use nor need for GeoGebra.
Proof 2 is by Leo Giugiuc.
Borislav Mirchev has also posted this problem on a different forum and proposed an analogues relation involving excentral and extouch triangles. (The extouch triangle is formed by the points of tangency of the excircles with the sides of the base riangle.)
Let $(I_a),(I_b),(I_c)$ be the excircles of $\Delta ABC$ that touch the sides $BC,AC,AB$ in points $A_{1},B_{1},C_{1},$ respectively. Then
$[\Delta ABC]^{2}=[\Delta A_{1}B_{1}C_{1}]\cdot [\Delta I_{a}I_{b}I_{c}].$
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73581773
