Reflection in a Triangle Tangent to Parabola
Experimental Mathematics
What Might This Be About?
Theorem
Let the three sidelines $BC,CA,AB$ of $\Delta ABC$ be tangent to a parabola at $A_1,B_1,C_1,$ respectively. Let $A'$ be the reflection of $A$ in the midpoint $M$ of $BC.$
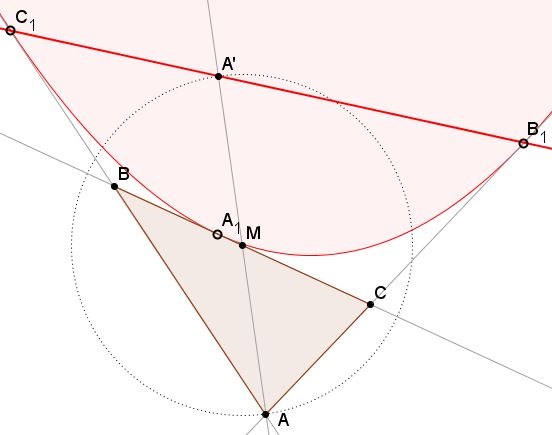
Prove the three points $B_1,C_1,A'$ are collinear.
Proof
In a Cartesian coordinate system, let the parabola have equation:
$y=px^2.$
The points of tangency are then expressed as $A_1=(a,pa^2),$ $B_1=(b,pb^2),$ $C_1(c,pc^2),$ for some real $a,b,c.$ From here we obtain the equations of the sideline of $\Delta ABC$ as the tangents at points $A_1,B_1,C_1$:
$\begin{align} l_{BC}:\,&y=2pax-pa^2\\ l_{CA}:\,&y=2pbx-pb^2\\ l_{AB}:\,&y=2pcx-pc^2 \end{align}$
Solving these in pairs we obtain the Cartesian coordinates of $A,B,C:$ $\displaystyle A=(\frac{b+c}{2},pbc),$ $\displaystyle B=(\frac{a+c}{2},pac)$, $\displaystyle C=(\frac{a+b}{2},pab).$
Now, me can find first $\displaystyle M=M_a(\frac{a}{2}+\frac{b+c}{4}, \frac{pac+pab}{2})$ and then $A'=(a, pab+pac-pbc).$
Finally,
$\begin{align} B_{1}A'=(a-b,pb^2-pab-pac+pbc)=p(a-b)(1,-b-c),\\ C_{1}A'=(a-c,pc^2-pab-pac+pbc)=p(a-c)(1,-b-c), \end{align}$
which are obviously collinear.
Extra Problem
Let $B_2$ be the reflection of $B_1$ in $C;$ $C_2$ be the reflection of $C_1$ in $B.$ Then the four points $A',$ $A_1,$ $B_2,$ and $C_2$ are collinear.
Acknowledgment
The theorem, its proof and the extra problem have been posted by Dao Thanh Oai (Vietnam) at the CutTheNotMath facebook page. Observe that the theorem is a clear generalization of a lemma by Archimedes, which is the above statement when $M=A_1.$
Conic Sections > Parabola
- The Parabola
- Archimedes Triangle and Squaring of Parabola
- Focal Definition of Parabola
- Focal Properties of Parabola
- Geometric Construction of Roots of Quadratic Equation
- Given Parabola, Find Axis
- Graph and Roots of Quadratic Polynomial
- Greg Markowsky's Problem for Parabola
- Parabola As Envelope of Straight Lines
- Generation of parabola via Apollonius' mesh
- Parabolic Mirror, Theory
- Parabolic Mirror, Illustration
- Three Parabola Tangents
- Three Points on a Parabola
- Two Tangents to Parabola
- Parabolic Sieve of Prime Numbers
- Parabolic Reciprocity
- Parabolas Related to the Orthic Triangle
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73582356
