Not So Hidden Homotheties

What Might This Be About?

Problem

Circles $(O)$ and $(P)$ are tangent at $A;$ circles $(O)$ and $(Q)$ are tangent at $B;$ $C$ is a point on $(O).$ $J$ is the second intersection of $AC$ with $(P);$ $L$ is the second intersection of $BC$ with $(Q).$

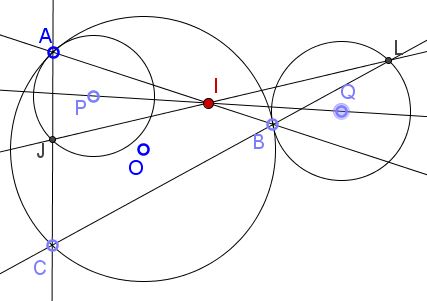
Not So Hidden Homotheties - problem

Prove that the three lines $PQ,$ $AB$, and $JL$ are concurrent.

Hint

The problem has several solutions; the one I find especially revealing makes use of the salient presence of homotheties.

Solution

Let $H_{A}(X),$ $H_{B}(X)$ be the homotheties with centers $A$ and $B,$ respectively such that $H_{A}(J)=C$ and $H_{B}(C)=L.$ Naturally, more is true: $H_{A}((P))=(O)$ and $H_{A}((O))=(Q).$

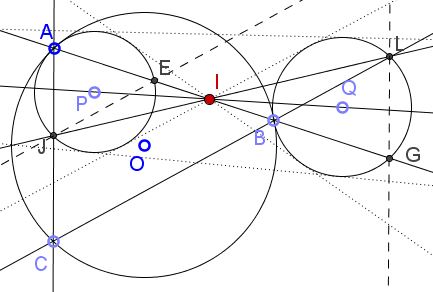
Not So Hidden Homotheties - solution

As we know, the product of homotheties - if not a translation - is again a homothety with the center on the line joining the centers of the two given homotheties. But $H_{B}(H_{A}(P)=(Q)),$ implying that the product of $H_{A}$ and $H_{B}$ is a homothety with center at one of the centers of similitude of circles $(P)$ and $(Q).$

Further, $H_{B}(H_{A}(A)=H_{B}(A)=G$ and $H_{B}(H_{A}(J)=H_{B}(C)=L$ from which it follows that $AG$ (read $AB$) and $JL$ both pass through the center, say $I,$ of the homothety $H_{B}(H_{A}(X)).$

The point of concurrence $I$ is independent of the choice of $C.$

For other solutions see an onlne discussion.

Acknowledgment

The problem has been posted by Dao Thanh Oai (Vietnam) at the CutTheKnotMath facebook page.

Geometric Transformations

72187077