Spiral Similarity and Collinearity

The following problem has been posted by Dao Thanh Oai at the CutTheKnotMath facebook page

Assume triangles $AB_1C_1,$ $AB_2C_2,$ and $AB_3C_3$ are similar. Then, if $B_1B_2B_3$ are collinear so are $C_1C_2C_3.$

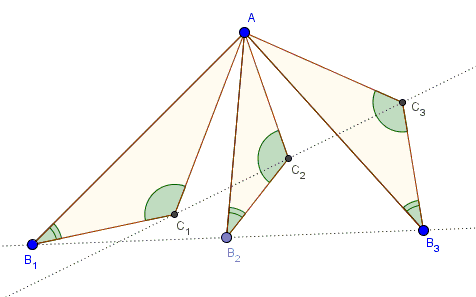
Below is a dynamic illustration of the concept:

22 January 2015, Created with GeoGebra

The statement could be derived with some effort from the Fundamental Theorem of Directly Similar Figures. But using the same technique (complex numbers) the explanation is straightforward.

Let's place $A$ at the origin and use $p$ as the complex number corresponding to $B_1.$ Choose any two complex numbers, say, $u$ and $v$. Recollect that multiplication by a complex number amounts to a rotation (corresponding to its argument) combined with a homothety (corresponding to its modulus), i.e. a spiral similarity. Assume $p,$ $up,$ and $vp$ are collinear, which is expressed as, say:

$\displaystyle\frac{p-up}{p-vp} \space\mbox{is a real number}.$

However, $\displaystyle\frac{p-up}{p-vp}=\frac{1-u}{1-v}$ independent of $p$ such that if $p,$ $up,$ and $vp$ are collinear for one $p,$ they are collinear for any other.

To solve the problem stated at the top of the page, observe that for the three similar triangles, if $B_2$ and $B_3$ are obtained by two spiral similarities from $B_1$ then it is also true that $C_2$ and $C_3$ are obtained by the same two spiral similarities from $C_1.$ In fact, this is true for all corresponding points in the triangles: midpoiints of sides, centroids, orthocenters, circumcenters, etc.

Geometric Transformations

Plane Isometries
Plane Isometries As Complex Functions
Affine Transformations (definition)
- Homothety - an Affine Transform
  - Geometric Problems by Homothety
- What Is Shear Transform?
- Spiral Similarity
  - Construction of the center of spiral similarility
  - Spiral Similarity and Collinearity
Inversion
- Stereographic Projection and Inversion
- Möbius Transformations
Projective transformation (definition)

49551892