Dao's Archimedean Twins
What Might This Be About?
Problem
If $R_1$ and $R_2$ are the respective radii of $O_1$ and $O_2$ then circles with the radius $\displaystyle r=\frac{R_{1}R_{2}}{R_{1}+R_{2}},$ are known as Archimedean due to one of Archimedes' discoveries.
Semicircles $(O_1)$ and $(O_2)$ are drawn on diameters $AC$ and $BC,$ respectively, $C$ being a point on segment $AB.$ $D$ is the midpoint of the arc $AC$; $(E)$ the midpoint of the arc $BC.$ Lines $AE$ and $CD$ cross at $F;$ $BD$ and $CE$ cross at $G.$ $F',G'$ are projections of $F,G$ on $AB.$ Also, $I$ is the second intersection of $AE$ with $(O_2);$ $H$ is the second intersection of $BD$ with $(O_1).$
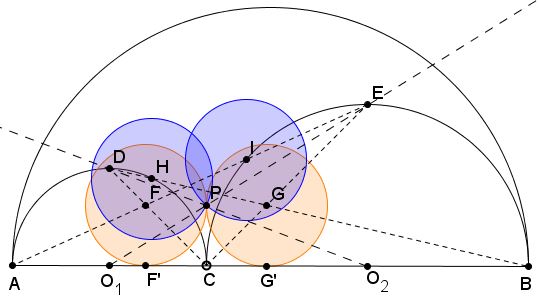
Then
$FF'=GG'=CF'=CG'=r,$
Circles $F(r)$ and $G(r)$ centered at $F$ and $G$ with radius $r$ are Archimedean, tangent at $P,$
Circles $H(P)$ and $I(P)$ centered at $H$ and $I$ through $P$ are Archimedean.
First pair
Triangles $AFF'$ and $AEO_2$ are similar from which
$\displaystyle\frac{FF'}{AF'}=\frac{EO_2}{AO_{2}}.$
With $CF'=x,$ this becomes $\displaystyle\frac{x}{2R_{1}-x}=\frac{R_2}{2R_{1}+R_{2}},$ from which $x=\displaystyle\frac{R_{1}R_{2}}{R_{1}+R_{2}}=r.$

Similarly, $GG'=r.$
Second Pair
I'll now use repeatedly the Power of a Point theorem to prove that points $C,F,H,I,G$ lie on circle $P(r)$ centered at $P$ and radius $r.$

First of all $AI\cdot AE=AC\cdot AB=4R_{1}(R_{1}+R_{2}).\space$ From the similiarity of triangles $AFF'$ and $AEO_{2},$ $\displaystyle\frac{AF}{AE}=\frac{FF'}{EO_{2}}=\frac{r}{R_2}.$ Multiplying the two gives
$\displaystyle AI\cdot AF=4R_{1}(R_{1}+R_{2})\cdot \frac{R_{1}R_{2}}{R_{2}(R_{1}+R_{2})}=4R_{1}^{2},$
which says that $I$ and $F$ belong to a circle with $AC$ as a tangent, i.e., a circle tangent to $AB$ at $C.$ The same naturally holds for $G$ and $H.$ But we already saw that points $F$ and $G$ likewise belong to a circle with the same property, namely, $P(r).$ It thus follows that all five points lie an that circle, because for every point $X\ne C$ there is a unique circle tangent to $AB$ at $C$ that passes through $X.$
In particular, $IP=HP=r.$
Acknowledgment
The above circles have been found by Dao Thanh Oai (Vietnam). The first pair is not new - it is found at #20 of Floor van Lamoen's catalog of the Archimedean twins. Dao Thanh Oai's construction is shorter and highlights new properties of the pair. The second pair of twins -Dao's twins - appears to be new.
- Arbelos - the Shoemaker's Knife
- 7 = 2 + 5 Sangaku
- Another Pair of Twins in Arbelos
- Archimedes' Quadruplets
- Archimedes' Twin Circles and a Brother
- Book of Lemmas: Proposition 5
- Book of Lemmas: Proposition 6
- Chain of Inscribed Circles
- Concurrency in Arbelos
- Concyclic Points in Arbelos
- Ellipse in Arbelos
- Gothic Arc
- Pappus Sangaku
- Rectangle in Arbelos
- Squares in Arbelos
- The Area of Arbelos
- Twin Segments in Arbelos
- Two Arbelos, Two Chains
- A Newly Born Pair of Siblings to Archimedes' Twins
- Concurrence in Arbelos
- Arbelos' Morsels
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73583258
