Proclivity of Conjoint Archimedean Twins for Proliferation
What Might This Be About?
A Discourse
This page is an outgrowth of an email by Emmanuel Antonio José García who came up with a realization that in case three Archimedean circles share a point, there is always - due to a theorem by R. A. Johnson - a fourth one through their pairwise intersections. Trivially, there is a fifth one centered at the common point of the three and passing through their centers.
Situations where several Archimedean circle concur at a point are well documented, especially in the online catalogue of Archimedean circles maintained by Floor van Lamoen. For example, in van Lamoen's notations, circles $A_2,$ $A_{5a},$ $A_{5b},$ $A_8,$ $A_{14},$ $A_{50a},$ $A_{50b}$ all pass through the inner point $C$ of an arbelos consisting of three semicircles, the big one $(AB),$ and two small ones $(AC)$ and $(CB).$
As a matter of fact, given two intersecting or tangent (that could be described as conjoint) Archimedean circles it is easy to employ García's insight to construct an infinite family of the Archimedean siblings. When two circles of equal radius are tangent, others can be constructed with centers at a hexagonal grid:
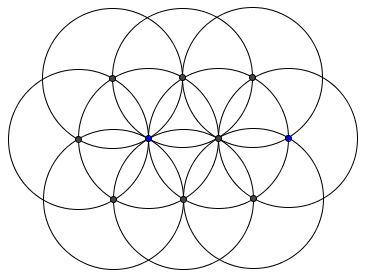
The construction starts with drawing a circle centered at the common point (the point of tangency in this case) and passing through the centers of the two circles. If there are two common points, either will serve our purpose but lead in general to a different Archimedean circle progeny. This circle intersects the given two in four points. Again, to continue we may choose any of the four points; as before, our choice will affect the resulting family of circles.
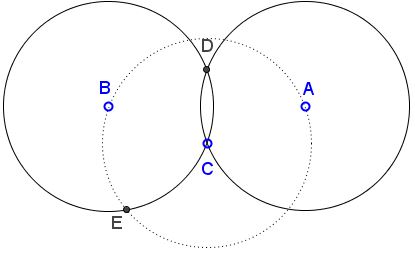
So, given two circle $(A)$ and $(B)$ of the same radius that meet in points $C$ and $D,$ draw circle $C(C,A),$ centered at $C$ through $A$ and, necessarily, through $B.$ Let $E$ be an intersection of $C(C,A)$ and $(B).$
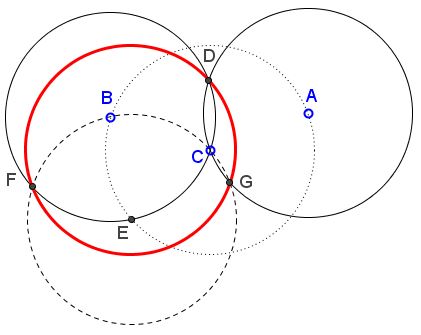
Now, draw circle $C(E,C),$ which intersects $(B)$ at $F$ and $(A)$ at $G.$ Since all circles constructed so far have the same radius, so, by Johnson's theorem, will circle $(DFG).$
This a diagram where I dared to consider all four intersections of $(C)$ and then repeat the steps with the four intersections of $(D).$ Needless to say that all the circles in the diagram have the same radius.
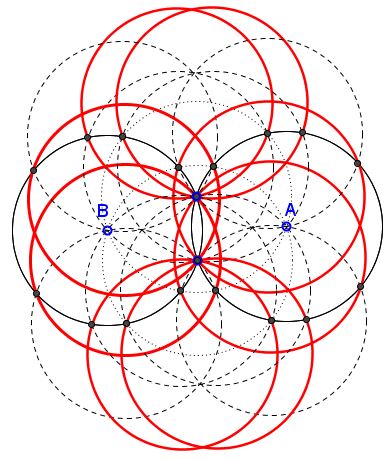
It may be interesting to investigate if and when different families of Archimedean circles may have to vie for custody of the same siblings.
- Arbelos - the Shoemaker's Knife
- 7 = 2 + 5 Sangaku
- Another Pair of Twins in Arbelos
- Archimedes' Quadruplets
- Archimedes' Twin Circles and a Brother
- Book of Lemmas: Proposition 5
- Book of Lemmas: Proposition 6
- Chain of Inscribed Circles
- Concurrency in Arbelos
- Concyclic Points in Arbelos
- Ellipse in Arbelos
- Gothic Arc
- Pappus Sangaku
- Rectangle in Arbelos
- Squares in Arbelos
- The Area of Arbelos
- Twin Segments in Arbelos
- Two Arbelos, Two Chains
- A Newly Born Pair of Siblings to Archimedes' Twins
- Concurrence in Arbelos
- Arbelos' Morsels
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73581437
