Another Pair of Archimedean Twins - a Redux
What Might This Be About?
Problem
For points $O,$ $O_1,$ $O_2$ on the segment $AB,$ let $(O),$ $(O_{1}),$ $(O_{2}),$ be semicircles with diameters $AB$, $AO$ and $OB,$ respectively, constructed on the same side. The area surrounded by the three semicircles is called arbelos. The perpendicular to $AB$ passing through $O$ divides the arbelos into two curvilinear triangles with congruent incircles. Circles congruent to those circles are said to be Archimedean
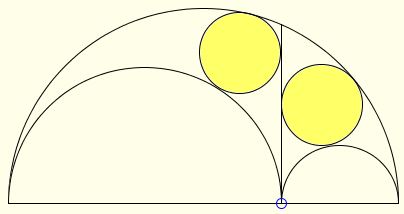
These were the subject of Archimedes' Lemma 5 from his famous Book of Lemmas.
Let $(R),$ $(R_{1}),$ $(R_{2})$ be the radii of $(O),$ $(O_{1}),$ $(O_{2}),$ respectively. The common radius $r$ of Archimedean circles is known to be
$\displaystyle r=\frac{R_{1}R_{2}}{R_{1}+R_{2}}.$
Let $D_i,$ $i=1,2,$ be points of intersection of $(O)$ with perpendicular bisectors of $AO$ and $OB.$ Let $E_{i}$ and $F_{i},$ $i=1,2$ be the points of intersections of lines from $A,$ $O$, and $B$ joining $D_{1}$ and $D_2$ as shown below.
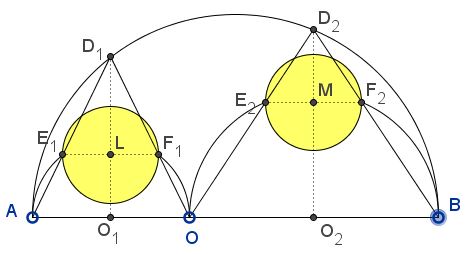
Then the circles on diameters $E_{i}F_{i},$ $i=1,2$ are Archimedean.
Solution
Just for the sake of reference, observe that $R=R_{1}+R_{2}.$
Consider homothety $h$ with center $B$ that maps $(O_{2})$ onto $(O).$ Then obviously, $h(F_{2})=D_2$, and the homothety has coefficient $\displaystyle\kappa =\frac{AB}{OB}=\frac{R}{R_{2}}.$
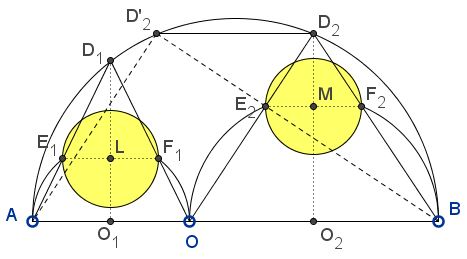
Triangles $BOD_2$ and $F_{2}E_{2}D_{2}$ are similar so that
$\displaystyle\frac{E_{2}F_{2}}{OB}=\frac{F_{2}D_{2}}{BD_{2}}=\frac{(\kappa -1)BF_{2}}{\kappa BF_{2}}=\frac{\kappa -1}{\kappa}=\frac{R_1}{R}.$
It follows that $\displaystyle E_{2}F_{2}=\frac{R_1\cdot OB}{R}=\frac{2R_{1}R_2}{R_{1}+R_{2}}$ - exactly the diameter of the Archimedean circle. Similarly, or due to the symmetry of the expression, $\displaystyle E_{1}F_{1}=\frac{2R_{1}R_2}{R_{1}+R_{2}}.$
Acknowledgment
I have two remarks concerning the note by paper by Hiroshi Okumura in the November 2013 issue of Mathematical Gazette which deals with the two Archimedean circles discussed above. Firstly, the article takes $D_{2}D'_{2}=AB-AO=2R_1$ for granted, and deduces from that
$\displaystyle E_{2}F_{2}=\frac{D_{2}D'_{2}}{\kappa}=\frac{2R_{1}R_2}{R_{1}+R_{2}}.$
I may be missing something but I do not immediately see why this is true. So the proof above is different from that in Mr. Okumura's note.
Secondly, I need to mention that the existence of this pair of the Archimedean twins was observed earlier by Quang Tuan Bui. This is certainly does not deny Mr. Okumura's discovery as independent.
References
- Arbelos - the Shoemaker's Knife
- 7 = 2 + 5 Sangaku
- Another Pair of Twins in Arbelos
- Archimedes' Quadruplets
- Archimedes' Twin Circles and a Brother
- Book of Lemmas: Proposition 5
- Book of Lemmas: Proposition 6
- Chain of Inscribed Circles
- Concurrency in Arbelos
- Concyclic Points in Arbelos
- Ellipse in Arbelos
- Gothic Arc
- Pappus Sangaku
- Rectangle in Arbelos
- Squares in Arbelos
- The Area of Arbelos
- Twin Segments in Arbelos
- Two Arbelos, Two Chains
- A Newly Born Pair of Siblings to Archimedes' Twins
- Concurrence in Arbelos
- Arbelos' Morsels
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73574317
