Second Pair of Twin Inequalities: Twin 1

Problem

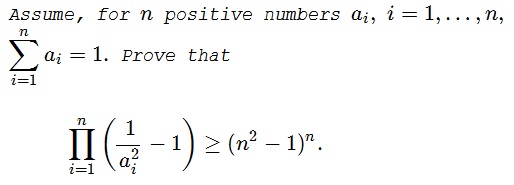
Solution 1

Due to the AM-GM inequality, the product $uv$ of two positive numbers with a fixed sum attains it's maximum when the numbers are equal. So the product grows as the two numbers approach each other while maintaining their sum.

It follows that, under the same convention, the expression

$\displaystyle\begin{align}\left(\frac{1}{u^2}-1\right)\left(\frac{1}{v^2}-1\right)&=\frac{1-u^2-v^2+u^2v^2}{u^2v^2}\\ &=\frac{1-(u+v)^2}{(uv)^2}+\frac{2}{uv}+1 \end{align}$

decreases.

Returning to the problem, if all numbers are equal to $\displaystyle \frac{1}{n},$ there is nothing to prove. Else, among positive numbers that sum up to $1,$ there bound to be one greater than $\displaystyle \frac{1}{n},$ the other less than $\displaystyle \frac{1}{n}.$ Let them move towards each other until one (or both) of them becomes $\displaystyle \frac{1}{n}.$ The product on the left of the inequality at hand may only decrease with this substitution. Continue this process while there are numbers different from $\displaystyle \frac{1}{n}.$ When there are none, i.e., when all $n$ numbers are equal, the left-hand side becomes exactly $(n^2-1)^n,$ while the original product is not less than that.

Solution 2

Assume we have $0\lt x\le y\le 1-x.$ Then

$\displaystyle \left(\frac{1}{x}-1\right)\left(\frac{1}{y}-1\right) \ge \left(\frac{2}{x+y}-1\right)^2.$

Indeed, this is equivalent to $\displaystyle ((y - x)^2 (x + y - 1))/(x y (x + y)^2)\le 0.$ Below is an illustration with wolframalpha:

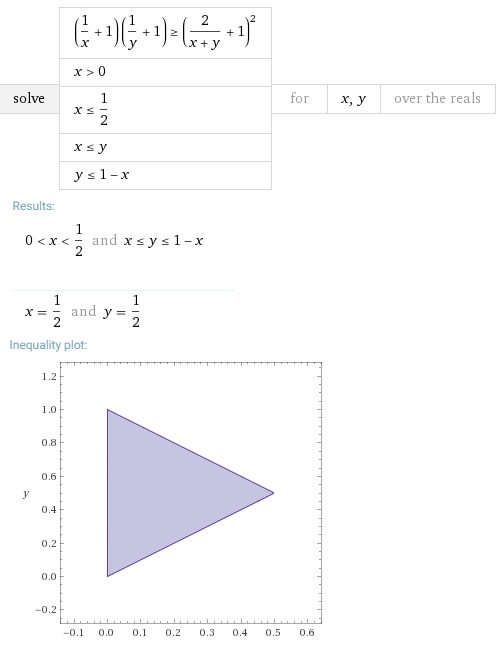
(1/x-1)(1/y-1) not less than (2/(x+y)-1)^2

Together with

$\displaystyle \left(\frac{1}{x}+1\right)\left(\frac{1}{y}+1\right) \ge \left(\frac{2}{x+y}+1\right)^2.$

we get

$\displaystyle \left(\frac{1}{x^2}-1\right)\left(\frac{1}{y^2}-1\right) \ge \left(\frac{2}{(x+y)^2}-1\right)^2.$

This justifies a step at a time process from Solution 1.

Acknowledgment

This is problem M1272 from the Kvant magazine (1991, nn 3,8). The problem and the solution are by L. Kurlyandchik. Solution 2 is by Christopher D. Long.

Inequalities with the Sum of Variables as a Constraint

An Inequality for Grade 8 $\left(\displaystyle\frac{1-x_1}{1+x_1}\cdot\frac{1-x_2}{1+x_2}\cdot\ldots\cdot\frac{1-x_n}{1+x_n}\ge\frac{1}{3}\right)$
An Inequality with Constraint $((x+1)(y+1)(z+1)\ge 4xyz)$
An Inequality with Constraints II $\left(\displaystyle abc+\frac{2}{ab+bc+ca}=p+\frac{2}{q}\ge q-2+\frac{2}{q}\right)$
An Inequality with Constraint V $\left(\displaystyle\prod_{k=1}^{n}x_k^{1/x_k}\le \frac{1}{n^{n^2}}\right)$
An Inequality with Constraint VI $\left(\displaystyle\prod_{k=1}^{n}\frac{1+x_k}{x_k}\ge \prod_{k=1}^{n}\frac{n-x_k}{1-x_k}\right)$
An Inequality with Constraint XI $(\sqrt{5a+4}+\sqrt{5b+4}+\sqrt{5c+4} \ge 7)$
Monthly Problem 11199 $\left(\displaystyle\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\ge\frac{25}{1+48abc}\right)$
Problem 11804 from the AMM $(10|x^3 + y^3 + z^3 - 1| \le 9|x^5 + y^5 + z^5 - 1|)$
Sladjan Stankovik's Inequality With Constraint $\left(abc+bcd+cda+dab-abcd\le\displaystyle \frac{27}{16}\right)$
Sladjan Stankovik's Inequality With Constraint II $(a^4+b^4+c^4+d^2+4abcd\ge 8)$
An Inequality with Constraint V $\left(\displaystyle\prod_{k=1}^{n}x_k^{1/x_k}\le \frac{1}{n^{n^2}}\right)$
An Inequality with Constraint VI $\left(\displaystyle\prod_{k=1}^{n}\frac{1+x_k}{x_k}\ge \prod_{k=1}^{n}\frac{n-x_k}{1-x_k}\right)$
An Inequality with Constraint XII $(abcd\ge ab+bc+cd+da+ac+bd-5)$
An Inequality with Constraint XIII $((3a-bc)(3b-ca)(3c-ab)\le 8a^2b^2c^2)$
Inequalities with Constraint XV and XVI $\left(\displaystyle\frac{a^2}{\sqrt{b^2+4}}+\frac{b^2}{\sqrt{c^2+4}}+\frac{c^2}{\sqrt{a^2+4}}\gt\frac{3}{5}\right)$ and $\left(\displaystyle\frac{a^2}{\sqrt{b^4+4}}+\frac{b^2}{\sqrt{c^4+4}}+\frac{c^2}{\sqrt{a^4+4}}\gt\frac{3}{5}\right)$
An Inequality with Constraint XVII $(a^3+b^3+c^3\ge 0)$
An Inequality with Constraint in Four Variables $\left(\displaystyle\frac{a^3}{b+c}+\frac{b^3}{c+d}+\frac{c^3}{d+a}+\frac{d^3}{a+b}\ge\frac{1}{8}\right)$
An Inequality with Constraint in Four Variables II $(a^3+b^3+c^3+d^3 + 6abcd \ge 10)$
An Inequality with Constraint in Four Variables III $\left(\displaystyle\small{abcd+\frac{15}{2(ab+ac+ad+bc+bd+cd)}\ge\frac{9}{a^2+b^2+c^2+d^2}}\right)$
An Inequality with Constraint in Four Variables IV $\left(\displaystyle 27+3(abc+bcd+cda+dab)\ge\sum_{cycl}a^3+54\sqrt{abcd}\right)$
Inequality with Constraint from Dan Sitaru's Math Phenomenon $\left(\displaystyle b+2a+20\ge 2\sum_{cycl}\frac{a^2+ab+b^2}{a+b}\ge b+2c+20\right)$
An Inequality with a Parameter and a Constraint $\left(\displaystyle a^4+b^4+c^4+\lambda abc\le\frac{\lambda +1}{27}\right)$
Cyclic Inequality with Square Roots And Absolute Values $\left(\displaystyle \prod_{cycl}\left(\sqrt{a-a^2}+\frac{1}{2\sqrt{2}}|3a-1|\right)\ge\frac{1}{6\sqrt{6}}\prod_{cycl}\left(\sqrt{a}+\frac{1}{\sqrt{3}}\right)\right)$
From Six Variables to Four - It's All the Same $\left(\displaystyle \frac{5}{2}\le a^2+b^2+c^2+d^2\le 5\right)$
Michael Rozenberg's Inequality in Three Variables with Constraints $\left(\displaystyle 4\sum_{cycl}ab(a^2+b^2)\ge\sum_{cycl}a^4+5\sum_{cycl}a^2b^2+2abc\sum_{cycl}a\right)$
Michael Rozenberg's Inequality in Two Variables $\left(\displaystyle \sqrt{x^2+3}+\sqrt{y^2+3}+\sqrt{xy+3}\ge 6\right)$
Dan Sitaru's Cyclic Inequality in Three Variables II $\left(\displaystyle \sum_{cycl}\sqrt{1+\frac{1}{a^2}+\frac{1}{(a+1)^2}}\geq \frac{9}{12-2(ab+bc+ca)}+3\right)$
Dan Sitaru's Cyclic Inequality in Three Variables IV $\left(\displaystyle \sum_{cycl}\frac{(x+y)z}{\sqrt{4x^2+xy+4y^2}}\le 2\right)$
Dan Sitaru's Cyclic Inequality in Three Variables VI $\left(\displaystyle \sum_{cycl}\left[\sqrt{a(a+2b)}+\sqrt{b(b+2a)}\,\right]\le 6\sqrt{3}\right)$
An Inequality with Arbitrary Roots $\left(\displaystyle \sum_{cycl}\left(\sqrt[n]{a+\sqrt[n]{a}}+\sqrt[n]{a-\sqrt[n]{a}}\right)\lt 18\right)$
Inequality 101 from the Cyclic Inequalities Marathon $\left(\displaystyle \sum_{cycl}\frac{c^5}{(a+1)(b+1)}\ge\frac{1}{144}\right)$
Sladjan Stankovik's Inequality With Constraint II $(a^4+b^4+c^4+d^2+4abcd\ge 8)$
An Inequality with Constraint in Four Variables $\left(\displaystyle\frac{a^3}{b+c}+\frac{b^3}{c+d}+\frac{c^3}{d+a}+\frac{d^3}{a+b}\ge\frac{1}{8}\right)$
An Inequality with Constraint in Four Variables IV $\left(\displaystyle 27+3(abc+bcd+cda+dab)\ge\sum_{cycl}a^3+54\sqrt{abcd}\right)$
Cyclic Inequality with Square Roots And Absolute Values $\left(\displaystyle \prod_{cycl}\left(\sqrt{a-a^2}+\frac{1}{2\sqrt{2}}|3a-1|\right)\ge\frac{1}{6\sqrt{6}}\prod_{cycl}\left(\sqrt{a}+\frac{1}{\sqrt{3}}\right)\right)$
From Six Variables to Four - It's All the Same $\left(\displaystyle \frac{5}{2}\le a^2+b^2+c^2+d^2\le 5\right)$
Michael Rozenberg's Inequality in Two Variables $(\displaystyle \sqrt{x^2+3}+\sqrt{y^2+3}+\sqrt{xy+3}\ge 6)$
Dan Sitaru's Cyclic Inequality in Three Variables II $\left(\displaystyle \sum_{cycl}\sqrt{1+\frac{1}{a^2}+\frac{1}{(a+1)^2}}\geq \frac{9}{12-2(ab+bc+ca)}+3\right)$
Dorin Marghidanu's Two-Sided Inequality $\left(\displaystyle \small{64(a+bc)(b+ca)(c+ab)}\le \small{8(1-a^2)(1-b^2)(1-c^2)}\le \small{(1+a)^2(1+b)^2(1+c^2)}\right)$
Problem 6 from Dan Sitaru's Algebraic Phenomenon $(x\sqrt{y+1}+y\sqrt{z+1}+z\sqrt{x+1}\le 2\sqrt{3})$
A Warmup Inequality from Vasile Cirtoaje $\left(a^4b^4+b^4c^4+c^4a^4\le 3\right)$
An Extension of the AM-GM Inequality $\left(x_{1}x_{2} + x_{2}x_{3} + x_{3}x_{4} + \ldots + x_{99}x_{100} \le \frac{1}{4}\right)$
- An Extension of the AM-GM Inequality: A second look $\left(x_{1}x_{2} + x_{2}x_{3} + x_{3}x_{4} + \ldots + x_{n-1}x_{n} \le \frac{a^2}{4}\right)$
Distance Inequality $\left(a^2+b^2+c^2\le\displaystyle\frac{9}{2}\right)$
Kunihiko Chikaya's Inequality with a Constraint $\left(4a^3+9b^3+36c^3\ge 1\right)$ An Inequality with Five Variables, Only Three Cyclic $\left(\displaystyle \left(a+\frac{b}{c}\right)^4+ \left(a+\frac{b}{d}\right)^4+ \left(a+\frac{b}{e}\right)^4\ge 3(a+3b)^4\right)$
Second Pair of Twin Inequalities: Twin 1 $\left(\displaystyle \prod_{i=1}^n\left(\frac{1}{a_i^2}-1\right)\ge (n^2-1)^n\right)$
Second Pair of Twin Inequalities: Twin 2 $\left(\displaystyle \prod_{i=1}^n\left(\frac{1}{a_i}+1\right)\ge (n+1)^{n}\right)$
Cyclic Inequality In Three Variables from the 2018 Romanian Olympiad, Grade 9 $\left(\displaystyle \frac{a-1}{b+1}+\frac{b-1}{c+1}+\frac{c-1}{a+1}\ge 0\right)$
Dan Sitaru's Cyclic Inequality in Three Variables IX $\left(\displaystyle \sum_{cycl}\sqrt{(x+y+1)(y+z+1)}\le 6+\sum_{cycl}\frac{x^3+y^3}{x^2+y^2}\right)$
Vasile Cirtoaje's Cyclic Inequality with Three Variables $\left(\displaystyle \sqrt{\frac{a}{b+c}}+\sqrt{\frac{b}{c+a}}+\sqrt{\frac{c}{a+b}}\ge 2\right)$ Leo Giugiuc and Vasile Cirtoaje's Cyclic Inequality $\left(\displaystyle \sqrt{\frac{a}{1-a}}+\sqrt{\frac{b}{1-b}}+\sqrt{\frac{c}{1-c}}+\sqrt{\frac{d}{1-d}}\ge 2\right)$

71544267