Möbius' Strip

Möbius' strip (or Möbius' band) is named after August Ferdinand Möbius (1790-1868). This is probably the most famous of all one-sided surface. Years ago, I create a short animation that illustrated the creation of a Möbius' strip from a piece of paper. It is still there and it still works but the passage of time left its marks. By today's standards, the movie does not impress one as it did at the end of the past century.

Schoolwise, Möbius' strip falls into the category of the cut & glue (& perhaps, again, cut) paper activities. There are several shapes that can be easily created from a paper strip. Alongside of more conventional cylinder and torus, one can create Möbius' strip and imagine Klein Bottle and Projective Plane that do not exactly fit in the 3-dimensional space.

To create a cylinder, take a strip of paper, bent it to join the two ends. For Möbius' strip, the procedure is rather the same, except, before joining the ends, turn one of them half a turn, i.e. 180°, and then apply glue. How does one verify that the resulting shape is one-sided? Draw the midline without lifting the pen! When finished, check that locally the line appears on both sides of the strip.

As was noted elsewhere, cutting Möbius' strip also leads to unexpected results.

The applet below, provides an illustration for the paper strip activities. It shows the shapes that can be obtained from a strip of paper by joining the ends after a number of half turns. Dragging the mouse (with the left button down) cause the shape to rotate. Clicking the left button stops the rotation. The shape consists of rectangular patches, N is the number of patches along the strip, M is the number of patches across. Each patch is of course a 2-sided shape, with the sides painted in greenish and bluish cues. Right-clicking on the greenish side makes it disappear. (Right click again to bring it back.) As a result, it is possible to obtain the shapes like the ones below:

	1 half turn, M = 3, the middle layer removed	2 half turns, M = 3, the middle layer removed

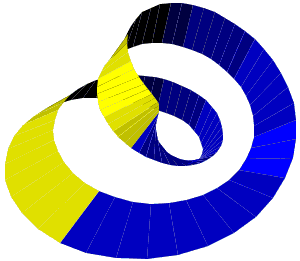
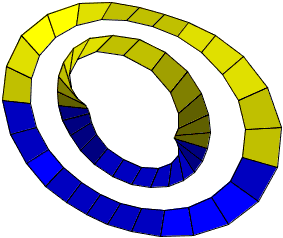
And here is the applet.

Can you figure out how to obtain the following configurations. (The right one is a trefoil knot.)

References

1. J. Fauvel, R. Flood, R. Wilson, Möbius' and His Band, Oxford University Press, 1993