Models and Metamathematics

All mathematical theories, in so far as they are based on a system of axioms and rules of deduction, are abstract constructs. For example, on an abstract level, in Projective Geometry, there is no way to distinguish between two kinds of objects, points and lines. Sentences in a mathematical theory are neither true nor false, only deducible (derivable, provable) or not.

However, mathematics is neither developed nor used as an abstraction. In practice, abstraction is only employed as a means of communication and classification of mathematical knowledge. For derivation and novel development, mathematicians rely on intuition based on interpretation of the otherwise abstract objects. The theories still remain abstract but, through interpretation, acquire meaning beyond what is formally ensconced in their formal settings. In addition to the grammar - the formal rules - interpretation endows a theory with semantics, making it meaningful for the sentences of the theory to become true or false.

The relation between a theory and its interpretation can be and was formalized leading to a mathematical theory whose subject is mathematical theory. As such, the former is usually known as metamathematics - a part of mathematics that deals with mathematics foundations, theories and models. A model is a mathematical theory endowed with interpretation. A theory may have a multitude of models as its objects may be interpreted in a variety of ways.

The set of all integers with operations of addition and subtraction is a model for an abstract Group Theory, as is the set of all non-zero rational numbers with operation of multiplication. There are groups of matrices, functions, points of algebraic curves - you name it.

The relation between a theory and a model is straightforward: a sentence derivable in the theory, is derivable in any of its models. Once interpreted, a derivable sentence becomes true. Being able to prove the negation of a sentence in the theory, makes it false in any interpretation. For the first-order theories, a stronger result holds. For a sentence not formally derivable in a first-order theory there is a model of the theory in which the interpretation of the sentence is false. This is known as Godel's Completeness Theorem.

A theory in which it is impossible to logically derive a contradiction, i.e. a sentence and its negation, is called consistent. A theory is called satisfiable if it admits a model (in which all its sentences are true.) Since in any possible interpretation a contradiction is false, every satisfiable theory is consistent. In theory which is not satisfiable, i.e., which admits no model, any sentence is derivable, for there is no model in which it may be false. In particular, a contradiction is derivable, meaning that such a theory can't be consistent.

The above gives a good idea of what metamathematics is about. But let's put the notions just introduced to an immediate use.

In Euclidean geometry there is a single line parallel to a given line and passing through a given point (not on a given line.) In the geometry of Lobachevsky and Bolyai the number of such lines is infinite. Is there a contradiction? No. Neither the Fifth Postulate nor its negation can be derived from the axioms of the Absolute Geometry. Moreover, there are models of Lobachevsky-Bolyai geometry within the Geometry of Euclid, implying that, in so far as the Euclidean geometry is consistent, so is the geometry of Lobachevsky-Bolyai.

There are three well known models of this sort. In two, the notion of a point is interpreted as a point inside an open disk, i.e., a set of points at a distance less than a given radius from a fixed point. Let's call the disk Γ.

The first model was proposed by E. Beltrami in 1868 and later popularized by F. Klein. A line in this model is any chord (less the end points) of Γ. There is only one line through any two points P, Q and there is infinitely many line parallel to PQ through a given point X:

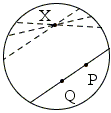
Klein's model of hyperbolic geometry

To clarify the significance of this construction let's call points in this model hpoints (to remind that Lobachevsky-Bolyai's geometry is also known as hyperbolic), the lines hlines, the circles hcircles, the angles hangles. There is little difference between points and hpoints, lines and hlines, circles and hcircles, and no difference at all between angles and hangles. The differences (where there are any) are in that the elements of the model are confined to Γ: hpoints are the points that lie inside Γ, hlines are pieces of the common (straight) lines that lie inside Γ and the same holds for hcircles. A circle that lies completely inside Γ is an hcircle; otherwise, hcircle is the arc of the circle that is inside Γ.

Let's check Euclid's Postulates. The first one says that any two points can be joined by a straight line. This is clearly holds for hpoints and hlines.

The second postulate says that a (finite) straight line can be produced beyond its endpoints. This is true for hlines because the points on the boundary of Γ are excluded from consideration; they do not exist in this model. Let the Euclidean line PQ intersect the boundary of Γ in S and T. Then the hline PQ can be extended beyond both P and Q by choosing arbitrary points between S and P or Q and T ( and there are plenty of those.) The process may never end because it will never lead to the S or T themselves.

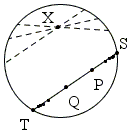
Enpoints are unreachable in Klein's model of hyperbolic geometry

The third postulate says that it is possible to describe a circle with any center and any radius. This is certainly so in so far as this is possible in the Euclidean geometry.

The fourth postulate says that all right angles are equal. Again, this is true for the hangles as long as this is true for the angles.

The fifth postulate obviously does not hold.

Where does it all lead us? First of all, assuming the Euclidean geometry consistent, the existence of the Beltrami-Klein model implies the consistency of the hyperbolic geometry where there are many parallels to a given line through a given point. Secondly, we may conclude that the Fifth Postulate is not a logical consequence of the first four. If it were, it would be true in every model of the Absolute Geometry (i.e., geometry built on top of the first four postulates.) The Beltrami-Klein model is one where this is not so, implying independence of the Fifth Postulate from the first four.

It's worth noting that in the above we looked simultaneously at a couple of formal theories (formal geometries based on four or five of Euclid's postulates.) In general, if a theory T₂ contains all the axioms of theory T₁ and yet some, we say that T₂ is richer than T₁. It is important to understand that any model of a richer theory T₂ is also a model of T₁. Naturally, any sentences provable in a theory is also provable in any richer theory.

As was mentioned before, there is another model of the hyperbolic geometry in Γ different from Beltrami-Klein's, although this one is also restricted to Γ. The model has been developed H. Poincaré. The lines now are the pieces of circles orthogonal to Γ.

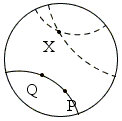
Poincare's model of hyperbolic geometry

The third model of the hyperbolic geometry is embedded into the upper half-plane, again with the border - the x-axis - excluded. The straight lines are the semicircles with centers on the x-axis. Of course one such model would suffice to realize the (relative) consistency of the hyperbolic geometry.

Back to What Is Infinity?

References

R. Courant, H. Robbins, What Is Mathematics?, Oxford University Press, 1996
D. Marker, Logic and Model Theory, in T. Gowers (ed.), The Princeton Companion to Mathematics, Princeton University Press, 2008, pp. 635-646
A. Robinson, Non-standard Analysis, Princeton University Press (Rev Sub edition), 1996
R. M. Smullyan, First-Order Logic, Dover, 1995
I. Stewart, Concepts of Modern Mathematicsc, Dover, 1995

71529869