Trilateral Diagrams

Lewis Carroll invented trilateral diagrams for the express purpose of resolving syllogisms. A trilateral diagram consists of two superimposed bilateral diagrams of different sizes. Three attributes are related to. As before, x and x' are expressed by horizontal rows of cells while y and y' are related to the vertical cell arrangement. A new attribute, m in Lewis Carroll's notation, is related to the inside of the middle square. Outer cells, i.e. cells outside of the middle square, relate to m'.

Usually, m and m' serve as eliminands, x and y as retinends. After two premises have been expressed on a diagram there is a way to eliminate m by collapsing the trilateral diagram into a bilateral diagram. Four "corner" squares are studied separately. Each "corner" square corresponds to a single square on a bilateral diagram. Depending on what combination of counters you find, you place (or do not place) a counter into the corresponding square of the bilateral diagram. Follow 3 rules:

1. If a square contains two gray counters, transfer one gray counter to the bilateral diagram.
2. If a square contains at least one red counter, transfer one red counter to the bilateral diagram.
3. In all other cases do nothing.

Let's present Euler's example in suitable notations:

• Premise 1: All x are m
• Premise 2: No y are m
• Hence, conclusion: No y are x

and see how trilateral diagrams work.

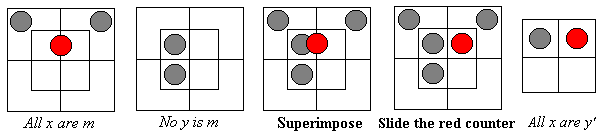
Note that, after superimposing the diagrams, the red counter slides from the fence as a gray counter to the left of it. In the North-West corner there are two gray counters one of which is passed on to the bilateral diagram (Rule 1). A red counter from the North-East corner is also inherited (Rule 2) by the bilateral diagram regardless of the presence of the gray counter. Nothing else is passed in accordance with Rule 3. The conclusion is All x are y' which is equivalent to the combination No xy exist and Some xy' exist.

Lewis Carroll

• Lewis Carroll's Logic Game (an introduction)
• Controversial Venn Diagrams
  • An Excerpt from The Science of Patterns
  • From W.Dunham, The Mathematical Universe
  • Venn Diagrams applet I
  • Venn Diagrams (an interactive activity)
• Bilateral Diagrams
  • Bilateral Diagrams (a comprehensive table)
  • Bilateral Diagrams (an interactive tool) Game
• Syllogisms
• Lewis Carroll's Logic Game (trilateral diagrams)
  • Interpretation of Trilateral Diagrams
  • Lewis Carroll's Logic Game (an interactive tool)
• Sample soriteses
• Lewis Carroll's Logic Game (rules and a tool)

|Contact| |Front page| |Contents| |Up| |Store|