An Excerpt from The Science of Patterns

Following is an excerpt from
MATHEMATICS: The Science of Patterns
by Keith Devlin

The nineteenth-century English mathematician John Venn invented a simple, geometric method for checking the validity of syllogisms, known nowadays as the method of Venn diagrams. In Venn's method, the syllogism is represented by means of three overlapping circles, as shown. The idea is that the region inside the circle marked S represents all objects of type S, and analogously for circles marked P and M. The procedure used to verify the syllogism is to see what the two premises say about various regions in the diagram, numbered 1 to 7.

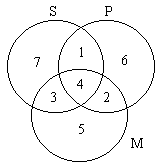
To illustrate the method, consider the simple example given in the text, namely, the syllogism

The major premise, All M are P, says that regions 3 and 5 are empty. (All the objects in M are in P, that is to say, are in the regions marked 2 and 4.) The minor premise, All S are M, says that regions 1 and 7 are empty. Thus, the combined effect of the two premises is to say that regions 1, 3, 5, and 7 are empty.

The goal now is to construct a proposition involving S and P that is consistent with this information about the various regions. Regions 1, 3, and 7 are empty, so anything in S Must be in region 4, and is therefore in P. In other words, all S are P. And that verifies this particular syllogism.

Though not all syllogisms are as easy to analyze as this example, all the other valid syllogisms can be verified in the same way.

Lewis Carroll

71543730