Bilateral Diagrams
Logic books of Lewis Carroll are more akin to Aristotle's Organon than to the Alice's series. Which would explain their lack of popularity. The books start with definitions of a series of terms: thing, attribute, adjunct, class, peculiar, genus, species, differentia, individual, dichotomy, name, definition, proposition, copula, predicate, terms, subject, normal from, particular, universal negative, universal affirmative, universe (of discourse).
While most of the words appear familiar, going through several pages of the definitions like "... Such a name is called 'Definition' of any Member of that Species, and to give it such a name is to 'define' it.", might have scared away a feeble hearted.
However, the idea is exactly the same as with Venn diagrams. A proposition describes a property of a group of objects (denoted by letters x,y, etc.) Objects are drawn from a convenient and meaningful (in a given context and given circumstances) universe of objects. Dichotomy relates to the convention that objects either may or may not have a certain property (attribute). (A man from a group of people can only be either young or not. Simultaneously, the man may or may not be middle aged. But, by convention, we will not consider the possibility of a single person being either young, or middle aged, or neither. This would be called a trichotomy.)
In the most popular of his logic books, The Game of Logic, Lewis Carroll writes in the style that endeared him to the generations of children and adults:
You will find these seven words - Proposition, Attribute, Term, Subject, Predicate, Particular, Universal - charmingly useful, if any friend should happen to ask if you have ever studied Logic. Mind you bring all seven words into your answer, and your friend will go away deeply impressed - 'a sadder and a wiser man.'
So objects (things) have properties, propositions state these properties, objects are drawn from a convenient set known as the universe. Here we are talking of simple propositions such that would correspond to a single circle on Venn diagrams.
As an example, cakes may be fresh or not. Three kinds of propositions can be stated in this context:
- Some cakes are fresh.
- No cakes are fresh.
- All cakes are fresh.
The Game of Logic starts very much like word problems: one has to introduce the variables, x's and y's. If x stands for the combination "fresh cakes" then the statement "Some cakes are fresh" is equivalent to saying that "Some x exist". And this is an example of what Lewis Carroll calls a particular proposition. For it talks only about a part of a set. "No cakes are fresh" is first rewritten as "No fresh cakes exist" and, then, as "No x exist". Depending on context, we may choose as the universe of discourse the set of all fresh cakes in which case "All cakes are fresh" is true or false depending on whether or not "some x exist".
Another possibility is to consider "All cakes are fresh" is an acceptable shorthand for "All cakes are fresh cakes" which is the same as "All y are x". Similarly, "No cakes are fresh" might have been shrunk to "no y are x", while "Some cakes are fresh" is converted to "Some y are x". It's noteworthy that "All y are x" implies "Some y are x", and actually stands for a combination of two: "Some y are x" and "No y is no x" ("No cake is no fresh cake"). In the latter examples, a natural universe of discourse is the set of all cakes.
With the introduction of negative statements we can as well consider statements like "Some cakes are not fresh" which begs for a notation for "not fresh cakes". With x standing for "fresh cakes", Lewis Carroll uses x' to denote "not fresh cakes". Thus "Some cakes are not fresh" is interpreted as "Some y are x'".
Bilateral diagram is Lewis Carroll's device to represent the situation in which objects are considered that may or may not have two properties. For example, we may consider sets of "fresh cakes" and "good cakes". So that a cake may be fresh, or good, or neither, or both. Let x and y stand for "fresh cakes" and "good cakes", respectively. In the bilateral diagram, the upper row of cells relates to x while the lower row relates to x'. Similarly, the left two cells relate to y while the right two relate to y'. Presence of a property is designated by a red counter; absence of a property is designated by a gray counter.
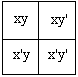
Putting a red counter into "xy" cell is an indication that "xy exist". In other words, "Some x are y" and "Some y are x" are equally true. Similarly, a red counter in the "xy'" cell means that "xy' exist", or "Some x are y'", or "Some y' are x". (Returning to our example, this would mean one of the following, "There exist fresh but not good cakes", or "Some fresh cakes are not good", and, lastly, "Some not good cakes are fresh".) A gray counter in the "xy" cell means that "No xy exist", which is "No x are y" and also "No y are x".
I placed a table of possible combinations and their interpretations on a separate page. Note that it's possible to place a red (but not a gray) counter on a partition between two adjacent cells. For example, "Some x exist" is symbolized by a red counter on the partition between "xy" and "xy'" cells which could also be interpreted as either "Some xy exist", or "Some xy' exist", or both. To express "No x exist" one needs two gray counters in the "xy" and "xy'" cells which is different from a disjunctive combination "No xy exist" or "No xy' exist".
Lewis Carroll
- Lewis Carroll's Logic Game (an introduction)
- Controversial Venn Diagrams
- Bilateral Diagrams
- Syllogisms
- Lewis Carroll's Logic Game (trilateral diagrams)
- Sample soriteses
- Lewis Carroll's Logic Game (rules and a tool)
|Contact| |Front page| |Contents| |Up|
Copyright © 1996-2018 Alexander Bogomolny73551010
