Brahmagupta's Formula and Theorem

Brahmagupta - an Indian mathematician who worked in the 7th century - left (among many other discoveries) a generalization of Heron's formula:

The area $S$ of a cyclic quadrilateral with sides $a, b, c, d$ is given by

$S = \sqrt{(s - a)(s - b)(s - c)(s - d)}$,

where s is the semiperimeter of the quadrilateral: $s = (a + b + c + d)/2.$

It is interesting to note that Heron's formula is an easy consequence of Brahmagupta's. To see that suffice it to let one of the sides of the quadrilateral vanish. On the other hand, Heron's formula serves an essential ingredient of the proof of Brahmagupta's formula found in the classic text by Roger Johnson.

Proof

Let the quadrilateral be $ABCD,$ with $AB = a,$ $BC = b,$ etc. Extend $AD$ and $BC$ to meet at $E,$ outside the circumcircle:

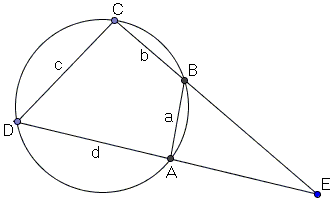
Brahmagupta's theorem for cyclic quadrilaterals

(If $AD\parallel BC$ then consider the other pair of the opposite sides. If those two are also parallel, the quadrlateral is a rectangle, and Brahmagupta's formula reduces to the standard formula for the area of a rectangle.)

Denote $x = CE$ and $y = DE.$ (I'll use the square brackets $[X]$ to denote the area of shape $X.)$ Apply Heron's formula to $\Delta CDE:$

$4\cdot [CDE] = \sqrt{(x + y + c)(x + y - c)(x - y + c)(-x + y + c)}.$

But triangles $ABE$ and $CDE$ are similar, implying:

$\displaystyle\frac{[ABE]}{[CDE]} = \frac{a^{2}}{c^{2}},$

from which

$\displaystyle\frac{S}{[CDE]} = \frac{c^{2} - a^{2}}{c^{2}}.$

We also have the proportions

$\begin{align} \displaystyle\frac{x}{c} &= \frac{y - d}{a}, \\ \frac{y}{c} &= \frac{x - b}{a}. \end{align}$

Adding the two and solving for $(x + y)$ gives

$x + y = c\displaystyle\frac{b + d}{c - a}.$

Similarly, subtracting one from the other and solving for $x - y$ we obtain

$x - y = c \displaystyle\frac{b - d}{c + a},$

from which we can find all the terms in Heron's formula. For example,

$\begin{align}\displaystyle x + y + c &= c\frac{b + d}{c - a} + c = c \frac{b + d + c - a}{c - a} = 2c \frac{s - a}{c - a},\\ x + y - c &= c \frac{b + d}{c - a} - c = c \frac{b + d - c + a}{c - a} = 2c \frac{s - c}{c - a},\\ x - y + c &= c \frac{b - d}{c + a} + c = c \frac{b - d + c + a}{c + a} = 2c \frac{s - d}{c + a}, \space\mbox{and}\\ -x + y + c &= - c\frac{b - d}{c + a} + c = c \frac{-b + d + c + a}{c + a} = 2c \frac{s - b}{c + a}. \end{align}$

A substitution then yields

$\displaystyle [CDE] = \frac{c^{2}}{c^{2} - a^{2}}\sqrt{(s - a)(s - b)(s - c)(s - d)}.$

And, finally,

$\displaystyle S = [CDE] \cdot \frac{c^{2} - a^{2}}{c^{2}} = \frac{c^{2} - a^{2}}{c^{2}}\frac{c^{2}}{c^{2} - a^{2}}\sqrt{(s - a)(s - b)(s - c)(s - d)}.$

Brahmagupta's formula follows.

References

R. A. Johnson, Advanced Euclidean Geomtry, Dover, 2007

Area of Quadrilateral

72352935