Area of a Bicentric Quadrilateral

A quadrilateral ABCD is bicentric if it is both inscriptible, i.e. admits an inscribed circle, and circumscriptible, i.e., cyclic - admits a circumscribed circle. The formula for the area of a cyclic quadrilateral has been discovered by the 7th century Indian mathematician Brahmagupta. In terms of the side lengths a, b, c, d and the semiperimeter s = (a + b + c + d)/2, the area of a cyclic quadrilateral is

S = √(s - a)(s - b)(s - c)(s - d),

or more explicitly,

4S = √(- a + b + c + d)(a - b + c + d)(a + b - c + d)(a + b + c - d).

For a bicentric quadrilateral, the formula allows for a significant simplification:

S = √abcd,

Proof

|Contact| |Front page| |Contents| |Geometry| |Store|

Copyright © 1996-2012 Alexander Bogomolny

For a bicentric quadrilateral with side lengths a, b, c, d, the area S is given by

S = √abcd,

Proof

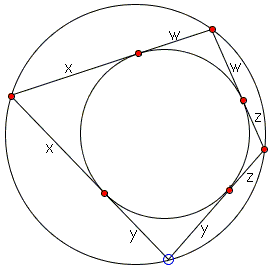
In a bicentric quadrilateral, the sides are each a sum of two adjacent tangents from the vertices to the inscribed circle. Denoting those tangents x, y, z, w, we can write, say,

a = x + y,
b = y + z,
c = z + w,
d = w + x.

The factors involved in the Brahmagupta's formula can be expressed differently:

- a + b + c + d = 2(w + z) = 2c,
a - b + c + d = 2(x + w) = 2d,
a + b - c + d = 2(y + x) = 2a,
a + b + c - d = 2(z + y) = 2b.

A substitution into Brahmagupta's formula gives

4S = √16abcd,

which is the required formula.

Area of Quadrilateral

• Brahmagupta's Formula and Theorem
• Carpets in a Quadrilateral
• Carpets in a Quadrilateral II
• Dividing Evenly a Quadrilateral
• Dividing Evenly a Quadrilateral II
• Area of a Bicentric Quadrilateral

|Contact| |Front page| |Contents| |Geometry| |Store|

Copyright © 1996-2012 Alexander Bogomolny