Simple Quadrilaterals Tessellate the Plane
A shape is said to tessellate the plane if the plane can be covered without holes and no overlapping (save for the boundary points) with congruent copies of the shape. Squares, rectangles, parallelograms, trapezoids tessellate the plane; each in many ways. Each of these can be arranged into an infinite strip with parallel sides, copies of which will naturally cover the plane.
A parallelogram is cut by either of its diagonals into two equal triangles. Conversely, two copies of the same triangle put next to each other after one of them has been rotated a half-turn form a parallelogram. Any triangle therefore also tessellates the plane. A honeycomb supplies a model of the hexagonal tessellation: a regular hexagon, too, tessellates the plane.
And this is almost it. Our list of tessellating shapes is almost complete. It can also be shortened. Squares, rectangles, parallelograms and trapezoids all are convex quadrilaterals with various degrees of regularity. However, no regularity is required of a quadrilateral to tessellate the plane: any simple, in particular a non convex, quadrilateral has this property.
The applet below allows you to experiment with arbitrary quadrilaterals. There is one present at the outset. Its shape can be modified by dragging its vertices. The buttons "Copy" and "Copy and rotate" help create copies if that basic shape. All so created polygons are draggable.
| What if applet does not run? |
|Activities| |Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander BogomolnyFirst note that copies and rotated copies of the quadrilateral taken in pairs fit snugly together as shown in the diagram.

The resulting (infinite) strip could be repeated indefinitely to cover the whole plane. This is because the sum of the angles of any quadrilateral is 360° - exactly the amount needed to fill the space around a point in the plane.

Note in passing that two copies of a quadrilateral - straight and rotated a half-turn - combine into a not necessary regular hexagon, but the one with opposite pairs of sides parallel and equal. We see that such polygons tessellate the plane.
Also, the medians of the quadrilaterals form a grid of congruent parallelograms.
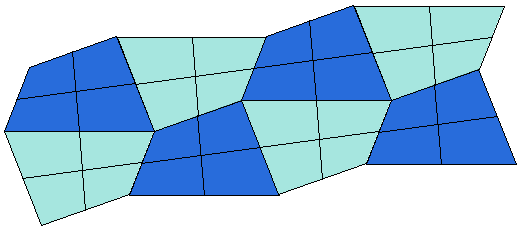
Douglas Rogers has observed that four copies of the quadrilateral that share a vertex form a tile that tessellates the plane in perhaps a more obvious way.

A grid is now formed by parallelograms 4 times as big whose area equals that of four reference quadrilaterals.
Below is a photograph of a outer house wall in New York City as may be observed from the City Highline.

References
- A. Engel, Problem-Solving Strategies, Springer Verlag, 1998, p. 323
- P. Hilton, D. Holton, J. Pederson, Mathematical Reflections in a Room with Many Mirrors, Springer Verlag, 1997
|Activities| |Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73607190
