Hippocrates' Squaring of a Lune

Hippocrates (470-410 B.C.) of Chios was probably the first to attempt an exposition of geometry in a logical manner. Although his tractates Elements has been lost, we do have some indirect information of the level of Hippocrates' knowledge of the subject. (According to Aristotle, Hippocrates showed extreme inaptitude in all walks of life except teaching of geometry. Thus he may serve as a counterexample to an argument that the study of geometry helps develop logical thinking in children.)

One of the results firmly associated with his name is known as the Quadrature of Lunes. A lune is a concave shape formed by two circular arcs (blue regions in the applet below.) Hippocrates actually managed to find the quadrature, i.e. the area, of the lunes of a very special kind. As was common with the Greeks, to find the quadrature meant constructing a square equal in area to a given shape using ruler and compass. Some sources mention that Hippocrates claimed being able to square a circle. But the common demonstration to this effect contains a simple logical error which a mathematician of such a caliber was unlikely to have overlooked.

Hippocrates began with an observation that the areas of two circles are in the same proportion as the squares of their radii. In Euclid's Elements this comes as Proposition XII.2 (Circles are to one another as the squares on their diameters) and is proved by Archimedes' method of exhaustion. In all likelihood, this is exactly the method employed by Hippocrates himself.

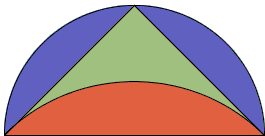
Following Hippocrates, we then find ourselves in the realm of Euclid's second proof of the Pythagorean Theorem, viz., Proposition VI.31: the areas of two semicircles on the legs of a right triangle add up to the area of the semicircle on the hypotenuse. For the sake of Hippocrates' argument, the semicircles on the legs are drawn externally and that on the hypotenuse internally to the triangle.

Dropping the common circular segments we see (by the Carpets Theorem) that the sum of the areas of two lunes equals the area of the triangle. In case, where two lunes are equal, each occupies the same area as one half of the triangle, now conveniently isosceles. Squaring of the lune in this case with ruler and compass is straightforward. (In the general case the lunes are known as the Lunes of Alhazen, the Latinized name of Abu Ali al-Hasan ibn al-Hasan ibn al-Haytham al-Basri (965-1040) who, among other endeavors, translated Ptolemy's Almagest and wrote on optics and lune quadratures.)

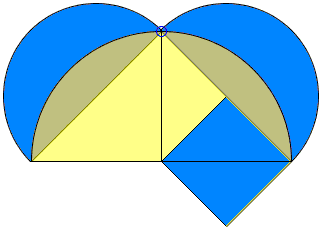
There is another way to obtain the same lune [Fauvel, p. 50]. Start with an isosceles right triangle and a semicircle on its base. The semicircle cuts off from the triangle two equal circular segments. A third segment similar to the first two is drawn on the base of the triangle. Its area equals that of the two small segments. It follows that the area of the lune formed by the two arcs, equals the area of the triangle.

References

1. W. Dunham, Journey through Genius, Penguin Books, 1991
2. J. Fauvel, J. Gray (eds), The History of Mathematics. A Reader, The Open University, 1987

Quadrature: A Child's Play

• Hippocrates' Squaring of a Lune
• Hippocrates' Squaring of Lunes
• Squaring a Rectangle
• Shearing a Polygon into a Triangle of Equal Area
• Triangle of Equal Area

Copyright © 1996-2008 Alexander Bogomolny