An ancient extra-geometric proof -

A special page commemorating the exhibition and sale of the Archimedes Palimpsest.

Scott E. Brodie

10/27/98

On October 27, 1998, the New York Times reported that Christie's auction house in New York City would shortly auction the "Archimedes Palimpsest", perhaps the most important single historical manuscript in the field of mathematics.

The manuscript is a "palimpsest" - a document written on recycled parchment: the original inscription (portions of several of the works of Archimedes) was erased (fortunately for us, only incompletely) so the valuable parchment could be re-used for a collection of Greek Orthodox prayers. It came to light about one hundred years ago, and was brought to the attention of J. L. Heiberg, perhaps the greatest student of the primary sources for classical Greek geometry, who studied it in Istanbul. He recognized, the "undertext" as the work of Archimedes, including portions of several works previously known from other manuscripts or translations, as well as a work, the Method, previously considered lost.

The Method proved a revolution in the understanding of Archimedes' thought. It provides a glimpse into the thinking which led Archimedes to many of his famous results, including the determination of the area of a parabola, the area and volume of a sphere, and the volume of an ellipsoid. Apparently, Archimedes, whose understanding of such matters as levers and centers of gravity was particularly insightful, was able to envision ways to "weigh" various geometric figures against one another so as to successfully compare their areas or volumes. In this sense, they are, perhaps, the original "extra-geometric" proofs. Notwithstanding the ingenious logic behind these demonstrations, Archimedes apparently considered them only informal ("back of the papyrus" ?) calculations, and preferred to publish these results with more formal double indirect proofs, now referred to as the "method of exhaustion."

As an instructive example, I have reproduced below the entire text of Proposition 2, which determines the volume of a sphere. (Proposition 1 determines the area of a segment of a parabola; I have skipped ahead to Proposition 2 because the geometric prerequisites are much more familiar.) Archimedes considered this theorem his greatest achievement, and directed that a schematic representation of it be placed on his tombstone.

From The Method of Archimedes (the translation is that of T.L. Heath):

Proposition 2.

We can investigate by the [mechanical] method the propositions that

Any sphere is (in respect of solid content) four times the cone with base equal to a great circle of the sphere and height equal to its radius; and

the cylinder with base equal to a great circle of the sphere and height equal to the diameter is 1½ times the sphere.

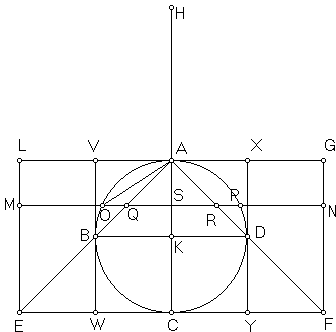
Let ABCD be a great circle of a sphere, and AC, BD diameters at right angles to one another.

Let a circle be drawn about BD as diameter and in a plane perpendicular to AC, and on this circle as base let a cone be described with A as vertex. Let the surface of this cone be produced and then cut by a plane through C parallel to its base; the section will be a circle on EF as diameter. On this circle as base let a cylinder be erected with height and axis AC, and produce CA to H, making AH equal to CA.

Let CH be regarded as the bar of a balance, A being its middle point.

Draw any straight line MN in the plane of the circle ABCD and parallel to BD. Let MN meet the circle in O,P, the diameter AC in S, and the straight lines AE, AF in Q, R respectively. Join AO.

Through MN draw a plane at right angles to AC; this plane will cut the cylinder in a circle with diameter MN, the sphere in a circle with diameter OP, and the cone in a circle with diameter QR.

Now, since MS = AC, and QS = AS,

MS·SQ	= CA·AS
	= AO²
	= OS² + SQ²

And, since HA = AC,

HA : AS	= CA : AS
	= MS : SQ
	= MS²: MS.SQ
	= MS²: (OS² + SQ²), from above,
	= MN²: (OP² + QR²)
	= (circle, diam. MN) : (circle, diam. OP + circle, diam. QR).

That is,

HA : AS = (circle in cylinder) : (circle in sphere + circle in cone).

Therefore the circle in the cylinder, placed where it is, is in equilibrium, about A, with the circle in the sphere together with the circle in the cone, if both latter circles are placed with their centres of gravity at H.

Similarly for the three corresponding sections made by a plane perpendicular to AC and passing through any other straight line in the parallelogram LF parallel to EF.

If we deal in the same way with all the sets of three circles in which planes perpendicular to AC cut the cylinder, the sphere, and the cone, and which make up those solids respectively, it follows that the cylinder, in the place where it is, will be in equilibrium about A with the sphere and the cone together, when both are placed with their centres of gravity at H.

Therefore, since K is the centre of gravity of the cylinder,

HA : AK = (cylinder) : (sphere + cone AEF).

But HA = 2·AK;

Therefore cylinder = 2 (sphere + cone AEF).

Now cylinder = 3 (cone AEF); [Eucl. XII 10]

Therefore cone AEF = 2 (sphere).

But, since EF = 2·BD,

Cone AEF = 8 (cone ABD);

Therefore, sphere = 4 (cone ABD).

Through B, D draw VBW, XDY parallel to AC;

and imagine a cylinder which has AC for axis and the circles on VX, WY as diameters for bases.

Then cylinder VY	= 2 (cylinder VD)
	= 6 (cone ABD)[Eucl XII 10]
	= 3/2 (sphere), from above.

Q.E.D.

"From this theorem, to the effect that a sphere is four times as great as the cone with a great circle of the sphere as base and with height equal to the radius of the sphere, I conceived the notion that the surface of any sphere is four times as great as a great circle in it; for, judging from the fact that any circle is equal to a triangle with base equal to the circumference and height equal to the radius of the circle, I apprehended that, in like manner, any sphere is equal to a cone with base equal to the surface of the sphere and height equal to the radius."

Reference

The Works of Archimedes with the Method of Archimedes, edited by T. L. Heath, Dover Publications, New York, 1953.

P.S.

The Archimedes Palimpsest was sold on October 29, 1998 at Christie's to "an unidentified American Collector" for $2,000,000. A spokesman for Christie's said the new owner will make the manuscript available for study by scholars.

49632954