Parallelogram and Similar Triangles
What is this about?
A Mathematical Droodle

Explanation

|Activities| |Contact| |Front page| |Contents| |Geometry|

Copyright © 1996-2018 Alexander Bogomolny

The applet is intended to suggest the following proposition:

Note that the statement is a double generalization of a problem by V. Thébault. For one, the square is replaced by a parallelogram. Also, two equilateral triangles are replaced by a pair of arbitrarily shaped similar triangles.

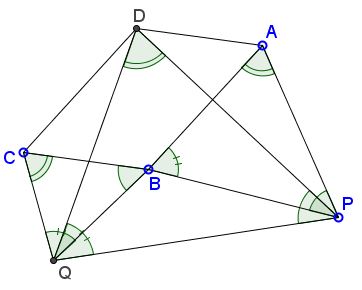
Proof 1

To say that "triangles PAB and BCQ are similar" means precisely that

∠PAB = ∠BCQ = α say,
∠ABP = ∠CQB and
∠BPA = ∠QBC.

Moreover, we know also that PA/BC = AB/CQ (since the two triangles are automatically proportional). In the parallelogram we know that BC = AD and AB = DC, so that we have

PA / AD = DC / CQ.

Since opposite angles in a parallelogram are equal we have ∠BAD = ∠BCD = β say, so

∠DAP = ∠DCQ = α + β.

Hence, using SAS version of similarity, triangles PAD and DCQ are similar, so ∠APD = ∠CDQ = γ say, and ∠ADP = ∠CQD = δ say. From triangle DCQ we have

α + β + γ + δ = 180°

(angles in a triangle). Since ∠ADC + ∠BCD = 180° (adjacent angles in a parallelogram), we conclude that

∠PDQ = α.

Since triangles PAD and DCQ are similar, we have

PA / PD = DC / DQ = AB / DQ,

so PA / AB = PD / DQ. Finally, since ∠PAB = ∠PDQ = α, we conclude that triangles PAB and PDQ are similar (SAS version of similarity.)

Proof 2

Let K be the intersection of the diagonals in the parallelogram and L and M the midpoints of BP and BQ respectively. Then triangle KLM is similar to triangles APB and CBQ by the Three Similar Triangles Theorem. Triangles KLM and DPQ are similar as having pairwise parallel sides.

Proof 3

William McWorter has noticed that the linear combinations in Proof 2 can be replaced with common vector (or affine) sums. Taking B as the origin, we have D = A + C, P = P + B, and Q = B + Q, which makes ΔDPQ similar to ΔAPB and ΔCBQ directly, without the intermediate ΔKLM.

References

1. A. D. Gardiner, C. J. Bradley, Plane Euclidean Geometry: Theory and Problems, UKMT, 2005

|Activities| |Contact| |Front page| |Contents| |Geometry|