Maxwell's Theorem: What Is It?
A Mathematical Droodle

Maxwell's Theorem

The applet suggests the following theorem [Prasolov, 11.48, Pedoe, 6.1, 8.3, 28.4]:

Given ΔABC and a point P, the sides of ΔA'B'C' are parallel to the cevians in ΔABC through P. Prove that the cevians in ΔA'B'C' parallel to the sides of ΔABC are concurrent.

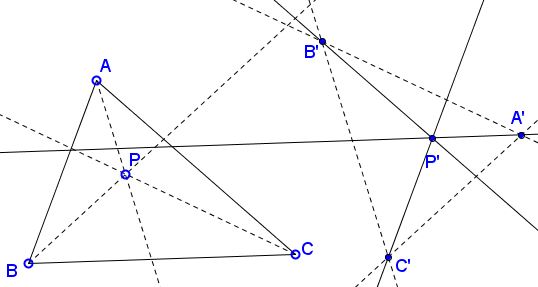
Maxwell's theorem

A similar statement is true if the lines are taken to be perpendicular, instead of parallel. Furthermore, the two are clearly equivalent. We'll prove the latter.

Triangles A'B'C' with sides parallel to the given set of cevians are all similar. It therefore sufficient to establish the theorem for any one of those triangles. Consider the circumcenters O_A, O_B, and O_C, of triangles PBC, PAC, PAB, respectively. The circumcircles of triangles PBC and PAC share chord PC, so that O_AO_B is perpendicular to PC. Similarly, O_AO_C ⊥ PB and O_BO_C ⊥ PA, which means that ΔO_AO_BO_C is one of the family A'B'C'. The lines through its vertices perpendicular to the sides of ΔABC are exactly the perpendicular bisectors of the latter, which are known to meet at a point.

Two triangles ABC and A'B'C' are said to be orthologic if perpendiculars from A, B, C to B'C', A'C', A'B' are concurrent. The point of concurrency is known as the orthologic center of ΔABC with respect to ΔA'B'C'. Maxwell's theorem justifies the symmetry of the definition: if the perpendiculars from the vertices of one of the triangle to the sides of the other are concurrent, then the perpendiculars from the vertices of the latter to the sides of the former are also concurrent. As an example, in any triangle, the associated medial and contact triangles are orthologic.

We can use complex variables and the real product [Andreescu, 4.1] of complex numbers to easily establish the perpendicular case of Maxwell's theorem. For two complex numbers u and v define the real product as

u·v = (uv* + vu*)/2,

where the asterisk denotes the complex conjugate. Assuming u = u₁ + iu₂ and v = v₁ + iv₂,

u·v = u₁v₁ + u₂v₂.

In other words, the real product of two complex numbers is exactly the scalar product of the 2D-vectors represented by these complex numbers. It follows that for four complex numbers u, U, v, V the lines joining them pairwise are perpendicular iff

(U - u)·(V - v) = 0.

Assume now the complex coordinates of the vertices of triangles ABC and A'B'C' are a, b, c and a', b', c'. The perpendicular from A to B'C' has the equation

(1)	(z - a)·(c' - b') = 0.

Similarly the perpendiculars from B and C are given by the equations

(2)	(z - b)·(a' - c') = 0 and (z - c)·(b' - a') = 0.

Adding the three up eliminates z:

(3)	a·(c' - b') + b·(a' - c') + c·(b' - a') = 0,

which is the condition for the perpendiculars from A, B, C to B'C', A'C', A'B' to be concurrent. Indeed, if (3) holds then, for any z,

(4)	(z - a)·(c' - b') + (z - b)·(a' - c') + (z - c)·(b' - a') = 0.

Now let's see if we can choose z the right way. First, for any z on the perpendicular from a to b'c', the first term in (4) vanishes. The choice of z as the intersection of the perpendiculars from a and b, eliminates the first two terms, which makes the third term also 0.

Importantly, (3) can be regrouped into

(3')	a'·(c - b) + b'·(a - c) + c'·(b - a) = 0,

in which the triangles switched the roles. (3') is the condition for the concurrency of the perpendiculars from A', B', C' onto the sides of triangle ABC. Q.E.D.

As an example, the pedal triangle of any point is orthologic to the base triangle. Also, Gergonne and medial triangles associated with the given one are orthologic.

Remark 1

The theorem bears name of James Clerk Maxwell, a famous physicist. His proof is different from anything above yet beautifully simple. He drew 4 pairwise intersecting circles centered at A, B, C and P. Taken by three, the circles define 4 radical centers. Let A' be the radical center of the circle centered at B, C, P. B', C', P' are defind cyclically. Then, say, A' and P' lie on the common chord of the circles B and C, which makes A'P' perpendicular to BC, etc.

Remark 2

There is another proof of Maxwell's theorem based on the notion of barycenter and another one of a generalization that shows surprisingly the projective nature of the theorem.

Remark 3

The dual to Maxwell's theorem has been formulated and proved only recently.

References

T. Andreescu, D. Andrica, Complex Numbers From A to ... Z, Birkhäuser, 2006
D. Pedoe, Geometry: A Comprehensive Course, Dover, 1970
V. V. Prasolov, Problems in Planimetry, v 1, Nauka, Moscow, 1986 (Russian)

Maxwell Theorem and orthologic triangles

71532426

Maxwell's Theorem: What Is It? A Mathematical Droodle