Maxwell's Theorem by Way of Trigonometric Ceva
For the record, in the morning (May 24, 2013) I have received a message from Sohail Farhangi:
To remind, Maxwell's theorem reads:
Given \(\Delta ABC\) and a point P, the sides of \(\Delta A'B'C'\) are parallel (perpendicular) to the cevians in \(\Delta ABC\) through P. Prove that the cevians in \(\Delta A'B'C'\) parallel (perpendicular) to the sides of \(\Delta ABC\) are concurrent.
To appreciate Sohail's insight here is the trigonometric form of Ceva's theorem:
In \(\Delta ABC\), cevians \(AD,\) \(BE,\) \(CF\) concur if and only if
\(\displaystyle \frac{\mbox{sin}(\angle ABE)}{\mbox{sin}(\angle CBE)} \cdot \frac{\mbox{sin}(\angle BCF)}{\mbox{sin}(\angle ACF)} \cdot \frac{\mbox{sin}(\angle CAD)}{\mbox{sin}(\angle BAD)} = 1, \)
As an additional prop, here are convenience diagrams for Maxwell's theorem:
The "Parallel" case
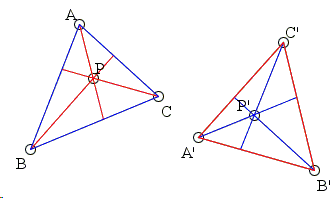
and the "perpendicular" case
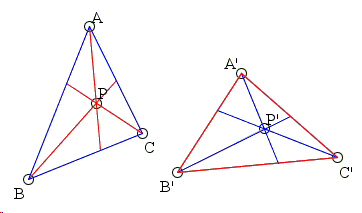
And the solution is ...
|Contact| |Front page| |Contents| |Geometry| |Up|
Solution
A simple fact about the two triangles is that the angles formed by the sides and the cevians in one are equal to the angles in the other, and this happens exactly as required in the trigonometric form of Ceva's theorem.
For example, in the parallel case,

\( \begin{align} \angle ABE &= \angle A'C'F' \\ \angle CBE &= \angle C'A'D' \\ \angle BCF &= \angle B'A'D' \\ \angle ACF &= \angle A'B'E' \\ \angle CAD &= \angle C'B'E' \\ \angle BAD &= \angle B'C'F', \end{align} \)
so that a substitution converts
\(\displaystyle \frac{\mbox{sin}(\angle ABE)}{\mbox{sin}(\angle CBE)} \cdot \frac{\mbox{sin}(\angle BCF)}{\mbox{sin}(\angle ACF)} \cdot \frac{\mbox{sin}(\angle CAD)}{\mbox{sin}(\angle BAD)} = 1 \)
to
\(\displaystyle \frac{\mbox{sin}(\angle A'C'F')}{\mbox{sin}(\angle C'A'D')} \cdot \frac{\mbox{sin}(\angle B'A'D')}{\mbox{sin}(\angle A'B'E')} \cdot \frac{\mbox{sin}(\angle C'B'E')}{\mbox{sin}(\angle B'C'F')} = 1. \)
After rearrangement this becomes
\(\displaystyle \frac{\mbox{sin}(\angle A'B'E')}{\mbox{sin}(\angle C'B'E')} \cdot \frac{\mbox{sin}(\angle B'C'F')}{\mbox{sin}(\angle A'C'F')} \cdot \frac{\mbox{sin}(\angle C'A'D')}{\mbox{sin}(\angle B'A'D')} = 1 \)
Exactly as stipulated by Ceva's theorem.
Maxwell Theorem and orthologic triangles
- Maxwell's Theorem
- Gergonne and Medial Triangles Are Orthologic
- Orthologic Triangles in a Quadrilateral
- Pedal Triangle and Isogonal Conjugacy
- Projective Proof of Maxwell's Theorem
- Maxwell's Theorem by Way of Trigonometric Ceva
|Contact| |Front page| |Contents| |Geometry| |Up|
Copyright © 1996-2018 Alexander Bogomolny73578927
