Square Inscribed in Triangle II:
What is this about?
A Mathematical Droodle

Explanation

|Activities| |Contact| |Front page| |Contents| |Geometry|

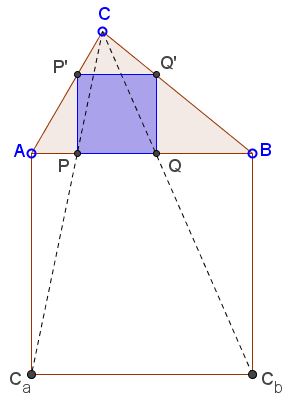
Here's a problem:

Construct on AB an associated Vecten square AC_aC_bB. Next, join C to both C_a and C_b and consider the points of intersection of CC_a and CC_b with AB. (In the applet they are denoted P and Q.)

I claim that PQ is the base of the sought square. To complete the square find points P' and Q' on AC and BC, respectively, such that PP'⊥ AB and QQ'⊥ AB.

There are several ways to view the configuration. An important thing to note is that there are three pair of similar triangles: ACC_a and P'CP, C_aCC_b and PCQ, and BCC_b and Q'CQ. The segments CP, CC_a, as well as, the segments CQ, CC_b are shared between two of those pairs. Therefore, the relevant side lengths ratios are all equal, which means that PP'Q'Q is indeed a square homothetic to C_aABC_b from C.

Under this homothety, the centers of the two squares correspond to each other and, therefore, are collinear with C. As a consequence, they are also collinear with one of the Vecten points. The problem has in general two solutions depending on whether we start with an outwardly or inwardly constructed Vecten square.

(Homothety can be also used to produce an entirely different solution.)

References

1. D. M. Bradley, On Shutting up and Listening, MAA Focus, (Jan 2009, v 29, n 1), pp. 20-21
2. F. van Lamoen, Inscribed Squares, Forum Geometricorum, Volume 4 (2004) 207-214

|Activities| |Contact| |Front page| |Contents| |Geometry|