Rectangle Inscribed in Triangle
What is this about? A Mathematical Droodle
Problem
Rectangle $XYY'X'\;$ is inscribed into $\Delta ABC,\;$ such that $X,Y\in BC,\;$ $X'\in AB,\;$ $Y'\in AC.$

Prove that center $K\;$ of the rectangle lies on the line $HM_a,\;$ where $H\;$ is the midpoint of the altitude $AH_a\;$ and $M_a\;$ the midpoint of $BC.$
Solution 1
$X'\;$ is a linear function of $X,\;$ $Y'\;$ is a linear function of $X',\;$ center $K\;$ is a linear function of $X\;$ and $Y',\;$ i.e., of $X.\;$ Thus when $X\;$ traverses a straight line ($AB\;$ specifically) so does $K.\;$ When $X\;$ coincides with $B,\;$ the rectangle degenerates into the segment $AB\;$ such that its center falls on $M_a.\;$ On the other hand, when $X\;$ coincides with the foot of the altitude $AH_a,\;$ the rectangle degenerates into the segment $AH_a\;$ an its center falls on the midpoint of $AH_a.\;$ Thus the locus of point $K\;$ is a part of line $HM_a\;$ covering that segment.
Solution 2
Extend $AX,AY\;$ to $AX_1,AY_1,\;$ with $BX_1\perp AB\;$ and $CY_1\perp AB.\;$ Figure $X_1Y_1CB\;$ is a homothetic image of rectangle $XYY'X'\;$ and is, therefore, also a rectangle.
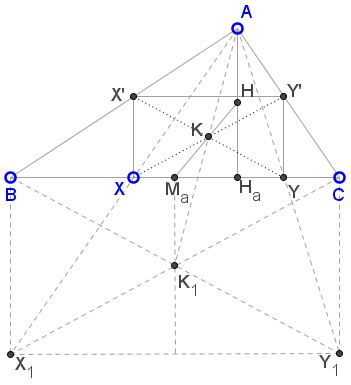
The centers of the two rectangles are homothetic as well. That of $X_1Y_1CB\;$ lies on the perpendicular bisector of $BC\;$ - a straight line. Thus, the locus of the center of $XYY'X'\;$ is also a straight line and, as before, it's $HM_a.$
Corollary
Lemoine point is located on $HM_a.$
Indeed, the antiparallels through the Lemoine point are equal and are divided by that point in half. Therefore, taken two by two, they form rectangles, one of which has a side on $BC\;$ and its center (which is the Lemoine point) on $HM_a.$
References
- Sammy Luo and Cosmin Pohoata, Let's Talk About Symmedians!, Mathematical Reflections 4 (2013), 1-11
Related material
| |
|
| |
|
| |
|
| |
|
| |
|Activities| |Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73578551
