A Double Meaning of an Arc's Midpoint

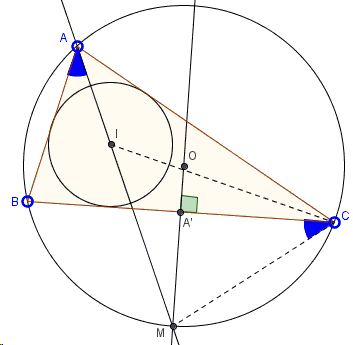
Let \(M\) be the midpoint of an arc of the circumcircle of \(\Delta ABC\) apposite vertex \(A\); let \(I\) denote the incenter of the triangle. Then \(M\), \(I\), and \(A\) are collinear. In addition, \(CM=IM\).

The applet below serves a dynamic illustration

Proof

A Double Meaning of an Arc's Midpoint

Proof

The proposition is a consequence of the definitions. The Incenter lies at the intersection of angle bisectors; in particular, it belongs to the angle bisector from \(A\).

On the other hand, equal inscribed angles are subtended by equal arcs, such that \(\angle BAI=\angle CAI\) implies that the (second) intersection of \(AI\) with the circumcircle is exactly the midpoint of the opposite arc \(\stackrel \frown {BC}\), which is \(M\).

Let angles at \(A\) and \(C\) be equal \(2\alpha\) and \(2\gamma\), respectively. Then, as an external angle of \(\Delta AIC\), \(\angle MIC=\alpha +\gamma\). But since inscribed angles \(BAM\) and \(BCM\) are both equal to \(\alpha\), \(\angle ICM=\alpha+\gamma\), implying \(\angle ICM=\angle MIC\) and making \(\Delta MIC\) isosceles, with \(CM=IM\).

It is worth noting that the excenters of a triangle have a similar property:

Let \(M\) be the midpoint of an arc of the circumcircle of \(\Delta ABC\) apposite vertex \(A\); let \(I_A\) denote the excenter of the triangle opposite A. Then \(M\), \(I_A\), and \(A\) are collinear. In addition, \(CM=I_{A}M\).

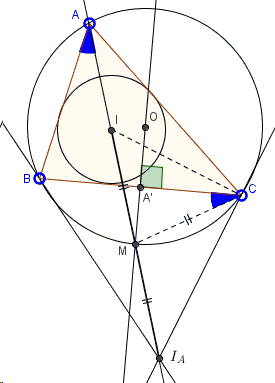
A Double Meaning of an Arc's Midpoint, now with an excenter

For one, \(\Delta ICI_A\) is right so that the median from \(C\) equals half the hypotenuse \(II_A\). Point \(M\) that forms an isosceles triangle \(CMI\) is unique on the hypotenuse (because the base angle \(MIC\) does not depend on the position of \(M\).) It follows that \(M\) is the midpoint of \(II_A\) which proves the claimed property of the excenters.

Note that the above supplies an alternative proof of the previously established fact that the midpoint of \(II_A\) lies on the circumcircle. As we've seen, this same point also serves as the midpoint of the arc of the circumcircle that is crossed by \(II_A\).

72371908