Generalizing a Romanian Olympiad Problem
What is this about?
A Mathematical Droodle

This applet requires Sun's Java VM 2 which your browser may perceive as a popup. Which it is not. If you want to see the applet work, visit Sun's website at https://www.java.com/en/download/index.jsp, download and install Java VM and enjoy the applet.

What if applet does not run?

Explanation

|Activities| |Contact| |Front page| |Contents| |Geometry|

Copyright © 1996-2018 Alexander Bogomolny

Elsewhere we discussed a problem from the 2001 National Romanian Olympiad:

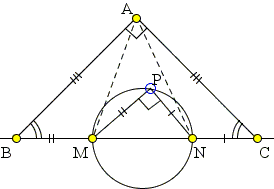
Consider the right isosceles triangle ABC and the points M, N on the hypothenuse BC in the order B, M, N, C such that BM² + NC² = MN². Prove that ∠MAN = 45°.

I find it more illuminating to have the diagram with P and A on different sides of MN:

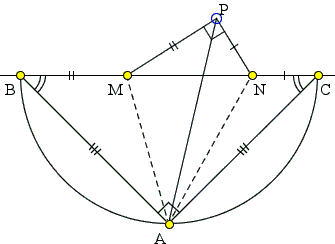
In this form the problem admits a significant generalization that, in particular, does away with the spurious Pythagorean condition:

Consider an isosceles triangle ABC and the points M, N on the base BC in the order B, M, N, C. Assume there is a point P such that MP = BM, PN = NC and ∠MPN = 2∠CBA. Then 2∠MAN + ∠MPN = 180°.

The Pythagorean condition BM² + NC² = MN² implies MP² + NP² = MN² making ΔMNP right at P, in which case the angle condition is equivalent to ∠MAN = 45°.

Let's reshuffle the construction a little and start with the ΔMPN. Given such a triangle, first find points A and B on opposite sides of the segment MN such that AM = MP and BN = NP. Next, form an isosceles triangle ABC, AB = AC with angles at the base equal half that of MPN. Then

(1)	2∠MAN + ∠MPN = 180°.

In this formulation, it is clear that as long as ∠MPN is fixed, so is ∠MAN. Therefore, if P stays on a circle through M and N so does A. The two circles are different, but not unrelated. The center Q of the circle traced by A lies on the circle traced by P and is the midpoint of the arc MN on the side of A. Q is also incident to the segment AP implying that AP bisects ∠MPN.

This applet requires Sun's Java VM 2 which your browser may perceive as a popup. Which it is not. If you want to see the applet work, visit Sun's website at https://www.java.com/en/download/index.jsp, download and install Java VM and enjoy the applet.

What if applet does not run?

Proof

Let B' and C' be the midpoint of BP and CP, respectively. Triangles BMP and CNP are isosceles. MB' is the bisector ∠BMP and is thus the external bisector of angle NMP. Similarly NC' is the external bisector of ∠CNP. These two lines meet the bisector of ∠MPN at the excenter of ΔMPN opposite vertex P, say A'. These same lines serve as perpendicular bisectors of sides MP and MP of ΔMPN and, as such, they meet on the perpendicular bisector of MN. For this point A', ΔCA'P is isosceles (A'C = A'P). Therefore, subtracting equal angles from equal angles, ∠A'PN = ∠A'CN. But ∠A'PN = ½∠MPN = ∠ACN, and we see that A' = A.

Further,

∠CPN = ∠NCP = ½∠MNP, ∠BPM = ∠MBP = ½∠NMP.

It follows that

∠B'PC' = ∠BPC   = ∠BPM + ∠MPN + ∠CPN   = ½∠MNP + ∠MPN + ½∠NMP   = 90° + ½∠MPN.

From (cyclic) quadrilateral AB'PC', with angles at B' and C' right, ∠B'AC' = 90° - ½∠MPN. Therefore,

∠MAN = 90° - ½∠MPN,

which is exactly (1).

When P traces a circle (i.e., when ∠MPN is fixed) so does A.

Related material Read more...
	Midpoints of the Lines Joining In- and Excenters
	Circles Tangent to Circumcircle
	60° Breeds 90°
	Cyclic Incenters
	Three Circles through the Incenter
	Circumcenter on Angle Bisector
	Euler's Formula and Poncelet Porism

|Activities| |Contact| |Front page| |Contents| |Geometry|

Copyright © 1996-2018 Alexander Bogomolny