Circumcenter on Angle Bisector
What Is It About?
A Mathematical Droodle

Created with GeoGebra

Explanation

|Activities| |Contact| |Front page| |Contents| |Geometry|

Copyright © 1996-2018 Alexander Bogomolny

The applet below provides an illustration to a problem from an outstanding collection by T. Andreescu and R. Gelca:

In ΔABC let I be the incenter. Prove that the circumcenter of ΔBIC lies on AI.

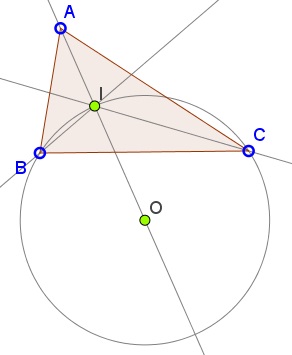
Circumcenter On Angle Bisector


I is the meeting point of the angle bisectors of ΔABC. In particular, AI is the angle bisector of ∠A. The excenter E opposite A, is the point of concurrency of AI and the exterior bisectors of angles at B and C.

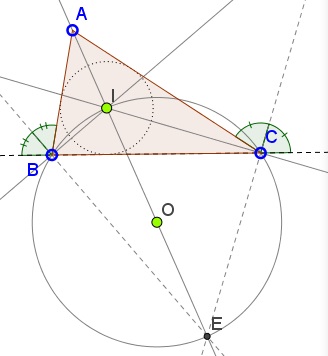
Circumcenter On Angle Bisector, proof

The latter are perpendicular to the angle bisectors BI and CI so that the quadrilateral BICE is cyclic and IE is a diameter of its circumcircle. Naturally, this is also the circumcircle of ΔBIC. Its center is the midpoint of IE and since A, I, and E are collinear, the conclusion follows.

It is also clear that the circumcenter O of ΔBIC lies on the circumcircle of ΔABC.

References

  1. T. Andreescu, R. Gelca, Mathematical Olympiad Challenges, Birkhäuser, 2004, 5th printing, 1.2.9 (p. 9)

Related material
Read more...

  • Midpoints of the Lines Joining In- and Excenters
  • Circles Tangent to Circumcircle
  • 60° Breeds 90°
  • Cyclic Incenters
  • Generalizing a Romanian Olympiad Problem
  • Three Circles through the Incenter
  • Euler's Formula and Poncelet Porism

    • |Activities| |Contact| |Front page| |Contents| |Geometry|

    Copyright © 1996-2018 Alexander Bogomolny

    72654213