Fuss' Theorem

The applet below illustrates Poncelet's porism for quadrilaterals. It is based on a formula by Nicolaus Fuss (1755-1826), a student and friend of L. Euler. Fuss also found the corresponding formulas for the bicentric pentagon, hexagon, heptagon, and octagon [Dörrie, p. 192].

 

This applet requires Sun's Java VM 2 which your browser may perceive as a popup. Which it is not. If you want to see the applet work, visit Sun's website at https://www.java.com/en/download/index.jsp, download and install Java VM and enjoy the applet.

What if applet does not run?

Explanation

|Activities| |Contact| |Front page| |Contents| |Geometry|

Copyright © 1996-2007 Alexander Bogomolny

The circumradius (R), the inradius (r) and the distance between the circumcenter and the incenter (d) of a bicentric quadrilateral stand in an elegant relationship

  1/(R - d)2 + 1/(R + d)2 = 1/r2,

It looks very much the same as Euler's formula for triangles, except for the exponent of 2.

Here's a very short proof of this fact by J. C. Salazar:

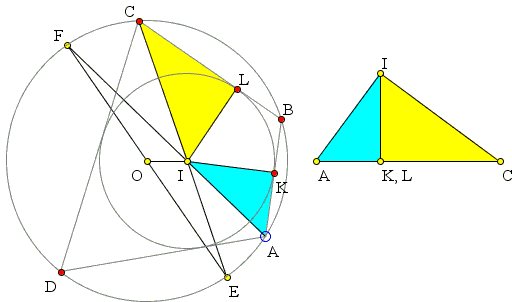
  Fuss' formula

Let the two circles be O(R) and I(r), K and L be the points where circle I(r) touches AB and BC.

Since quadrilateral ABCD is cyclic the angles at A and C are supplementary making angles BAI and ICB complimentary:

  ∠BAI + ∠ICB = 90°.

By construction, IK = IL = r. Two triangles AIK and CIL combined form a right triangle with legs AI and CI and the hypotenuse AK + CL. Its area can be found in two ways:

(1) r·(AK + CL) = AI · CI.

Also, the Pythagorean theorem applied to that triangle gives

(2) (AK + CL)² = AI² + CI².

From (1) and (2),

  r²·(AI² + CI²) = AI² · CI²,

or,

(3) 1/r² = 1/AI² + 1/CI².

Let AI and CI produced intersect O(R) in F and E. Then EF is a diameter of C(R) because

 
∠DOF + ∠DOE= 2(∠DAF + ∠DCE)
 = ∠BAD + ∠BCD
 = 180°.

We are then in a position to apply the formula for the length of a median (IO) in a triangle (EFI):

(4)
EI² + FI²= 2 IO² + EF² / 2
 = 2 (d² + R²).

Considering the diameter of O(R) through I, the intersecting chords theorem gives

(5) AI · FI = CI · EI = R² - d²

It follows (from (4) and (5)) that

(6)
1/AI² + 1/CI²= FI²/(R² - d²)² + EI²/(R² - d²)²
 = (EI² + FI²) / (R² - d²)²
 = 2 (R² + d²) / (R² - d²)².

Finally, from (3) and (6),

 
1/r²= 2 (R² + d²) / (R² - d²)²
 = [(R + d)² + (R - d)²)] / (R² - d²)²
 = 1/(R + d)² + 1/(R - d)².

References

  1. N. Altshiller-Court, College Geometry, Dover, 1980
  2. J. Casey, A Sequel to Euclid, Scholarly Publishing Office, University of Michigan Library (December 20, 2005), reprint of the 1888 edition, pp. 107-110
  3. J. L. Coolidge, A Treatise On the Circle and the Sphere, AMS - Chelsea Publishing, 1971, p. 45
  4. H. Dörrie, 100 Great Problems Of Elementary Mathematics, Dover Publications, NY,1965
  5. F. G.-M., Exercices de Géométrie, Éditions Jacques Gabay, sixiéme édition, 1991, pp. 837-839
  6. J. C. Salazar, Fuss' Theorem, The Mathematical Gazette, v 90, n 518 (July 2006), pp. 306-307.

Poncelet Porism

Related material
Read more...

Bicentric Quadrilateral

  • Collinearity in Bicentric Quadrilaterals
  • Easy Construction of Bicentric Quadrilateral
  • Easy Construction of Bicentric Quadrilateral II
  • Projective Collinearity in a Quadrilateral
  • Line IO in Bicentric Quadrilaterals
  • Area of a Bicentric Quadrilateral
  • Concyclic Incenters in Bicentric Quadrilateral

    • |Contact| |Front page| |Contents| |Geometry| |Eye opener|

    Copyright © 1996-2018 Alexander Bogomolny

    71873200