Square root of 2 is irrational
The statement we are going to discuss and prove is known as Theorem of Theaetetus due to its appearance in Plato's Theaetetus dialog:
Theaetetus: Theodorus was proving to us a certain thing about square roots, I mean the square roots of three square feet and five square feet, namely, that these roots are not commensurable in length with the foot-length, and he proceeded in this way, taking each case in turn up to the root of seventeen square feet; at this point for some reason he stopped. Now it occurred to us, since the number of square roots appeared to be unlimited, to try to gather them into one class, by which we could henceforth describe all the roots.
Socrates: And did you find such a class?
Theaetetus: I think we did; but see if you agree.
Socrates: Speak on.
Theaetetus: We divided all numbers into two classes. The one, consisting of numbers that can be represented as the product of equal factors, we likened in shape to the square and called them square or equilateral numbers.Socrates: And properly so.
Theaetetus: The numbers between these, among which are three and five and all that cannot be represented as the product of equal factors, but only as the product of a greater by a less or a less by a greater, and are therefore contained by greater and less sides, we likened to oblong shape and called oblong numbers.Socrates: Excellent. And what after this?
Theaetetus: Such lines as form the sides of equilateral plane numbers we called lengths, and such as form the oblong numbers we called roots, because they are not commensurable with others in length, but only with the plane areas which they have the power to form. And similarly in the case of solids.Below we shall concentrate on the one root -- that of 2 -- that Theaetetus has not mentioned and at times suggest an extension to a more general result. But first let's see how Richard Dedekind, one of the people most responsible for the current definition and understanding of irrational numbers, treated Theorem of Theaetetus:
Proof 1
Let $D$ be a positive integer but not the square of an integer, then there exists a positive integer $\lambda$ such that
$\lambda^{2} \lt D \lt (\lambda + 1)^{2}.$
... If there exists a rational number whose square is $D,$ then there exist two positive integers $t,$ $u,$ that satisfy the equation:
$t^{2} - Du^{2} = 0,$
and we may assume that $u$ is the least positive integer possessing the property that its square, by multiplication by $D,$ may be converted into the square of an integer $t.$ Since evidently
$\lambda u \lt t \lt (\lambda + 1)u,$
the number $v = t - \lambda u$ is a positive integer certainly less than $u.$ If further we put
$s = Du - \lambda t,$
$s$ is likewise a positive integer, and we have
$s^{2} - Dv^{2} = (\lambda^{2} - D)(t^{2} - Du^{2}) = 0,$
which is contrary to the assumption respecting $u.$ Hence the square of every rational number is either less than $D$ or greater than $D$ ...
Proof 2
A standard proof (e.g., [Rademacher and Toeplitz, Ch. 4]) of this result does not differ from the proof that $\sqrt{5}$ is irrational. Still, the argument can be modified a little.
The premise $p^{2} = 2q^{2}$ tells us that $p$ is even. Assuming $p$ and $q$ mutually prime, $q$ is bound to be odd. However, the square of an even number is divisible by $4,$ which leads us to conclude that $q$ is even. A contradiction.
Proof 3
Following is another intuitive one [Laczkovich, p. 4, Davis & Hersh, p. 299]. This one is based on the assertion that every number is uniquely (up to the order of factors) representable as a product of primes. (A prime is a number divisible only by itself and $1.)$ The fact which is known as The Fundamental Theorem of Arithmetic. Assuming it as an axiom (or a given fact), let $(p/q)^{2} = 2$ for some integers p and q. Then $p^{2} = 2q^{2}.$ Factor both $p$ and $q$ into a product of primes. $p^{2}$ is factored into a product of the very same primes as $p$ each taken twice. Therefore, $p^{2}$ has an even number of prime factors. So does $q^{2}.$ Therefore, $2q^{2}$ has an odd number of prime factors. Contradiction.
Proof 3'
Here's a modification that only counts the factors equal to $2$ [Automatic Sequences, p. 40]. $p^{2}$ has an even number of such factors, while $2q^{2}$ is bound to have an odd number of them. This is equivalent to saying that in the binary expansion of $p^{2}$ the number of unit digits is even, whereas on the right, in $2q^{2},$ the number of units is odd.
Proof 4
Following is yet another illuminating proof. As in the standard proof, assume $p$ and $q$ are mutually prime (numbers with no common factors). Their squares are still mutually prime for they are built from the same factors. Therefore, the fraction $p^{2}/q^{2}$ cannot cancel out. In particular, $p^{2}/q^{2}$ cannot cancel down to equal 2. Therefore, $p^{2}/q^{2}\ne 2.$
J. L. Lagrange in his Lectures on Elementary Mathematics (1898) argues that "... it's impossible to find a whole number which multiplied by itself will give $2.$ It cannot be found in fractions, for if you take a fraction reduced to its lowest terms, the square of this fraction will again be a fraction reduced to its lowest terms, and consequently cannot be equal to the whole number $2.$"
More than half a century earlier (1831), Augustus De Morgan explained that "... $7$ is not made by the multiplication either of any whole number or fraction by itself. The first is evident; the second cannot be readily proved to the beginner, but he may, by taking a number of instances, satisfy himself of this, that no fraction which is really such, that is whose numerator is not measured by its denominator, will give a whole number when multiplied by itself, thus $4/3\times 4/3 = 16/9$ is not a whole number, and so on."
The latter proof makes it entirely obvious that unless a square root of an integer is an integer itself, it is bound to be irrational. Furthermore, the same argument applies to roots other than square. Unless it's an integer itself, a fifth root of an integer is an irrational number!
The proofs above, directly or indirectly, appeal to the Fundamental Theorem of Arithmetic. In an article Irrationality Without Number Theory (Am. Math. Monthly, 1991), Richard Beigel set out to check how much of Number Theory is actually needed. He showed that for any integer $k$ and $t,$ $k^{1/t}$ is either integer or irrational using only the divisibility algorithm and the floor (whole part) function [n]. Following is his proof for $t = 2.$ (A more general result is shown to follow from the Rational Root Theorem and Gauss' Lemma. The latter has a proof that does not even mention the divisibility.)
Proof 5
Let $x = k^{1/2}$ and assume that $x$ is rational but not integer. Then there exists a minimal positive integer $n$ such that $xn$ is an integer. Consider $m = n(x - \lfloor x\rfloor).$ Since the fractional part of $x,$ $0 \le x - \lfloor x\rfloor \lt 1,$ $0 \le m \lt n.$ Note that $m$ is an integer for $m = nx - n\lfloor x\rfloor$ which is an integer. Furthermore, $mx = nx^{2} - (nx)\lfloor x\rfloor = nk - (nx)\lfloor x\rfloor$ which is also an integer. Due to the minimality of $n,$ $m = 0.$ In other words, $x = \lfloor x\rfloor$ and is, thus, an integer in contradiction to our assumption.
Richard's argument can be modified to invoke an infinite regression which is impossible for positive integers. Assuming $x$ to be rational, there exists an integer $n$ such that $nx$ is also an integer. As before, we can find an integer $m$ less than $n$ with the same property. $mx = 0$ gives an immediate contradiction. Otherwise, applying the same reasoning to $m$ and so on, we potentially have an infinite set of integers with no minimal element which is impossible. This is akin to the following geometric proof [Barbin, Gardner].
Proof 6

If $x = \sqrt{2}$ were rational, there would exist a quantity $s$ commensurable both with $1$ and $x:$ $1 = sn$ and $x = sm.$ (It's the same as assuming that $x = m/n$ and taking $s = 1/n.)$ The same will be true of their difference $x - 1,$ which is smaller than $x.$ And the process could continue indefinitely in contradiction with the existence of a minimal element. The game Euclid might have played always ends! As it does not, the algorithm leads to a continued fraction representation of $\sqrt{2}.$ The geometric form of the process is known as anthyphairesis which means (in Greek) continually subtract the smaller from the larger.
Proof 7
And here's another geometric proof I came across in an article by Tom Apostol (The American Mathematical Monthly, v 107, N 9, pp 841-842.) This one is so simple it may pass as a proof without words. But this is what his author had to say:
This note presents a remarkably simple proof of the irrationality of $\sqrt{2}$ that is a variation of the classical Greek geometric proof.
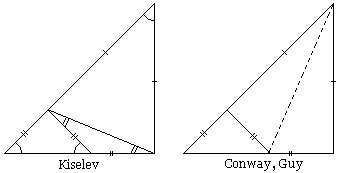
By the Pythagorean theorem, an isosceles right triangle of edge-length $1$ has hypotenuse of length $\sqrt{2}.$ If $\sqrt{2}$ is rational, some positive integer multiple of this triangle must have three sides with integer lengths, and hence there must be a smallest isosceles right triangle with this property. But inside any isosceles right triangle whose three sides have integer lengths we can always construct a smaller one with the same property, as shown below. Therefore $\sqrt{2}$ cannot be rational.

Construction. A circular arc with center at the uppermost vertex and radius equal to the vertical leg of the triangle intersects the hypotenuse at a point, from which a perpendicular to the hypotenuse is drawn to the horizontal leg. Each line segment in the diagram has integer length, and the three segments with double tick marks have equal lengths. (Two of them are tangents to the circle from the same point.) Therefore the smaller isosceles right triangle with hypotenuse on the horizontal base also has integer sides.
The reader can verify that similar arguments establish the irrationality of $\sqrt{n^{2} + 1}$ and $\sqrt{n^{2} - 1}$ for any integer $n \gt 1.$ For $\sqrt{n^{2} + 1}$ use a right triangle with legs of lengths $1$ and $n.$ For $\sqrt{n^{2} - 1}$ use a right triangle with hypotenuse $n$ and one leg of length $1.$
Essentially the same diagram has been used in a Russian geometry textbook by A. P. Kiselev, p. 121. The book, first published in 1892, has been in a systematic use up to the late 1950s with practically no competition, and frequently in the ensuing years. A proof to the same effect but with a paper folding interpretation is due to [Conway and Guy, pp. 183-185]
[Rademacher and Toeplitz, Ch. 4] gave two proofs of the irrationality of $\sqrt{2}$ of which the first was illustrated by practically the same diagram, without mention of the paperfolding background. As the starting point of the argument, they simply laid a side of a square on the diagonal and then proved the emergence of the smaller right isosceles triangle.
Proof 8
Assume [Laczkovich, Gardner] that $\sqrt{2} = p/q$ where $p$ and $q$ are the positive integers and $q$ is the smallest possible. Then $p \gt q$ and also $q \gt p - q,$ so that we have
$\begin{align} (2q - p)/(p - q) &= (2 - p/q)/(p/q - 1)\\ &= (2 - \sqrt{2})/(\sqrt{2} - 1)\\ &= (2 - \sqrt{2})(\sqrt{2} + 1)\\ &= \sqrt{2}. \end{align}$
But this contradicts the minimality of q.
(Prof. Claus I. Doering, Instituto de Matemática - UFRGS, Brazil, has pointed to a much earlier reference. The proof appeared in a footnote of the classic A Course of Modern Analysis by E. T. Whittaker and G. N. Watson, 4th Edition, Cambridge University Press, 1927. The footnote had also been included in the 3rd edition (1920).)
Proof 8'
Obviously, the proof can be restated as $(2p - q)^{2} = 2(p - q)^{2},$ which, too, is easily shown to hold, provided $p^{2} = 2q^{2}$ holds.
$\begin{align} (p - q)^{2}&= p^{2} - 2pq + q^{2}\\ &= 3q^{2} - 2pq,\\ (2q - p)^{2}&= 4q^{2} - 4pq + p^{2}\\ &= 3p^{2} - 4pq\\ &= 2(3q^{2} - 2pq)\\ &= 2(p - q)^{2}. \end{align}$
(Gary Davis has suggested an alternative formulation: If there is an integer $n > 0$ with $n\sqrt{2}$ an integer then $m = n(\sqrt{2} -1)$ has the same property, but is smaller than $n.)$
Proof 8''
A kindred proof has been published by Edwin Halfar (Am Math Monthly, Vol. 62, No. 6 (Jun-Jul 1955), p. 437). Suppose $\sqrt{2} = m/n,$ where $n$ and $m$ are positive integers. Then $n \gt m,$ and there is an integer $p \gt 0$ such that $n = m + p,$ and $2m^{2} = m^{2} + 2mp + p^{2}.$ This implies $m \gt p.$ Consequently, for some integer $a \gt 0,$ $m = p + a,$ $n = 2p + a$ and $2(p + a)^{2} = 2(p + a)^{2}.$ The last equality implies $a^{2} = 2p^{2}$ so that the entire process may be repeated indefinitely giving $n \gt m \gt a \gt p \ldots,$ but since every non-null set of positive integers has a smallest element, this is a contradiction and $\sqrt{2}$ is irrational.
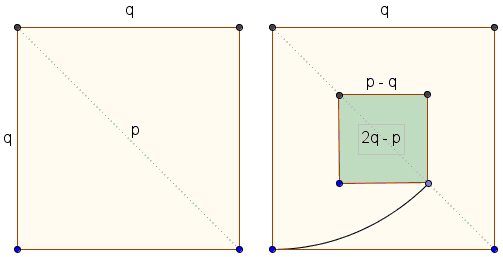
In plain English this asserts that given two squares with integer sides and one having twice the area of the other, there exist a pair of smaller squares with the same properties.
Proof 8'''
A superb graphic illustration for the latter has been popularized by J. Conway around 1990, see [Hahn, ex. 37 for Ch. 1]. Conway discussed the proof at a Darwin Lecture at Cambridge. The lecture appears alongside other Darwin lectures in the book Power published by Cambridge University Press. Conway's contribution is included as the chapter titled "The Power of Mathematics". The text can be found online. Conway attributes the proof to the Princeton mathematician Stanley Tennenbaum (1927 - 2006) who made the discovery in the early 1950s while a student at the University of Chicago.
Given two squares with integer sides, one twice the other

move the smaller squares

into opposite corners of the bigger square

The intersection of the two forms a square at the center of the diagram. Their union leaves two squares at the free corners of the diagram. By the Carpets Theorem, the two areas are equal:

(Obviously, these squares also have integer sides.)
Proof $8^{IV}$
Another illustration by Grant Cairns appeared in Math. Mag. 85 (2012), p. 123:
The first two steps of the infinite discent
are suggestive of the continuation
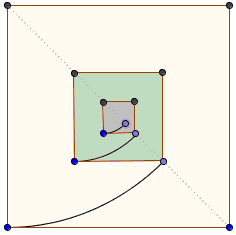
There are extensions of the geometric arguments to regular polygons other than the square that illustrate the irrationality of $\sqrt{3},$ $\sqrt{5},$ $\sqrt{6},$ and - in principle - of other square roots.
Proof $8^{V}$
Here's a variant from Am Math Monthly (120 (August/September) 2013, p 674) by Samuel G. Moreno and Esther M. García-Caballero:
If $\sqrt{2}$ is a rational number, then $x_{0}=\sqrt{2}+1$ is also rational, so $x_{0}=p/q,$ for some positive integers $p$ and $q$ with $q$ the smallest possible. Since $1\lt\sqrt{2}\lt 2,$ then $2\lt x_{0}\lt 3,$ which implies $2q\lt p\lt 3q.$ Clearly, $x_{0}(x_{0}-2)=(\sqrt{2}+1)(\sqrt{2}-1)=1,$ and thus
$\displaystyle\frac{1}{x_0}=x_{0}-2=\frac{p}{q}-2=\frac{p-2q}{q},$
so that $x_{0}=q/(p-2q).$ The bound $p-2q\lt q$ contradicts the minimality of $q.$
Proof 9
This proof is due to Alex Healy and was once available online at The Braden Files site. I owe the deepest thanks to Rick Mabry (Software Developer turned Professor) for pointing me in the right direction.)
Consider the set $W = {a + b \sqrt{2}},$ $a, b$ integers. Clearly $W$ is closed under multiplication and addition. Define $\alpha = (\sqrt{2} - 1),$ an element of $W.$ Obviously, $0 \lt \alpha \lt 1,$ so that
(1)
$\alpha ^{k} \rightarrow 0$ as $k\rightarrow\infty.$
Assume $\sqrt{2} = p/q.$ Since $W$ is closed, $\alpha ^{k} = e + f \sqrt{2} = (eq + fp)/q \ge 1/q$ contradicting (1).
(This proof has also appeared in an article Irrationality of Square Roots by P. Ungar, Math Magazine, v. 79, n. 2, April 2006, pp. 147-148, with an extension to roots of more general polynomials with integer coefficients, and [Laczkovich, pp. 4-5])
Proof 10
This proof too is by D. Kalman et al (Variations on an Irrational Theme-Geometry, Dynamics, Algebra, Mathematics Magazine, Vol. 70, No. 2 (Apr., 1997), pp. 93-104).
Let $A$ be the matrix
$A = \begin{pmatrix} -1 & \space 2\\ \space 1 & -1\\ \end{pmatrix}$
By the definition,
$ \begin{pmatrix} -1 & \space 2\\ \space 1 & -1\\ \end{pmatrix} \begin{pmatrix} a \\ b \end{pmatrix} = \begin{pmatrix} 2b-a \\ a-b \end{pmatrix} $
Two facts are worth noting: (a) matrix $A$ maps integer lattice onto itself, (b) the line with the equation $a = \sqrt{2}b$ is an eigenspace $L,$ say, corresponding to the eigenvalue $\sqrt{2} - 1:$
$ \begin{pmatrix} -1 & \space 2\\ \space 1 & -1\\ \end{pmatrix} \begin{pmatrix} \sqrt{2} \\ 1 \end{pmatrix} = \begin{pmatrix} 2-\sqrt{2} \\ \sqrt{2}-1 \end{pmatrix} =(\sqrt{2}-1) \begin{pmatrix} \sqrt{2} \\ 1 \end{pmatrix}. $
Since $0 \lt \sqrt{2} - 1 \lt 1,$ the effect of $A$ on $L$ is that of a contraction operator. So that the repeated applications of matrix $A$ to a point on $L$ remain on $L$ and approach the origin. On the other hand, if the starting point was on the lattice, the successive iteration would all remain on the lattice, meaning that there are no lattice points on $L.$
Proof 11
Conway and Guy (pp. 184-185) argue that if $\sqrt{N}$ is not an integer but a rational number $B/A,$ then
$B/A = NA/B.$
Assuming that $B/A$ in lowest terms, we observe that the fractional parts of $B/A$ and $NA/B$ have the form $a/A$ and $b/B,$ where $a,$ $b$ are positive integers smaller than $A,$ $B.$ But if two numbers are equal, their fractional parts are also equal:
$a/A = b/B$
so that
$b/a = B/A = \sqrt{N}.$
This gives a simpler form for $\sqrt{N},$ contrary to our assumption.
Proof 11'
Geoffrey C. Berresford (Am Math Monthly, Vol. 115, No. 6 (June-July 2008), p. 524) offered a different route from the assumption
$\sqrt{N} = B/A = NA/B,$
with $B/A$ in lowest terms.
If two fractions are equal, with one in lowest terms, the numerator and denominator of the other are a common integer (say $c)$ multiples of the numerator and denominator of the first. Therefore, $B = Ac,$ so that $B/A = c,$ and hence $\sqrt{N}$ is an integer, so $N$ is a perfect square.
(I am grateful to Prof. Claus I. Doering from Instituto de Matemática - UFRGS, Brazil for bringing this proof to my attention.)
Proof 12
Alan Cooper found what I would call a common-sense proof of the fact at hand. He based his proof on an observation that squaring a finite decimal fraction, say $m.n,$ never removes the decimal part. This becomes clear on considering the very last (non-zero) digit. This is the only digit responsible for the last digit in the decimal expansion of the square. Thus the latter is never zero.
In case where the fraction is not a finite decimal, we may switch to another number system in which the fraction is finite. The same argument now applies.
Alan notes that the above is a way of interpreting Proof 4.
Proof 13
Following Nick Lord (Math Gazette, v 91, n 521, July 2007, p. 256) we shall show that, for an integer $N \gt 1,$ $\sqrt{N}$ is irrational. The proof is based on the assertion that, for integer $a, m, n,$ $n \gt 1,$ $m$ and $n$ coprime, the expression
$m/n + an/m$
is never an integer. Indeed, if say $m/n + an/m = k,$ for an integer $k,$ then
$m^{2} = n\cdot (km - an),$
which would imply that $n$ divides $m$ - in contradiction with either $n \gt 1$ or coprimality of $n$ and $m.$
Assume then that $\sqrt{N}$ is rational but not an integer. Then, since $\sqrt{N} + 1$ is not an integer, we must have
$\sqrt{N} + 1 = m / n,$
for coprime $m$ and $n,$ with $n \gt 1.$ But the observation above with $a = 1 - N$ then leads to a contradiction that
$2 = \sqrt{N} + 1 + (1 - N) / (\sqrt{N} + 1)$
is not an integer.
Proof 14
Gustave Robson (Am Math Monthly, Vol. 63, No. 4 (Apr., 1956), p. 247) published a short proof preceded by a remark: The following proof was invented by Robert James Gauntt, in 1952, while he was a freshman at Purdue. I was unable to induce him to write up his proof.)
$a^{2} = 2b^{2}$ cannot have a non-zero solution in integers because the last non-zero digit of a square, written in the base three, must be $1,$ whereas the last non-zero digit of twice a square is $2.$
Proof 14'
This proof is by Stuart Anderson.
In $\mathbb{Z}_{3},$ the field of residues modulo $3$, $0^{2} = 0,$ $1^{2} = 1$ and $2^{2} = 1,$ so there is no element whose square is $2.$ Now suppose $\sqrt{2}$ is a rational number $a = p/q.\;$ Then $a$ maps to $p\;\mbox{(mod }3)$ / $q\;\mbox{ (mod }3),$ which is either $p$ or $2p\;\mbox{ (mod }3).\;$ It follows that $a^{2} = p^{2} \ne 2\;\mbox{ (mod }3)).\;$ But since reduction $\mbox{mod}\space 3$ respects all the arithmetic operations, $a^{2} = 2\;$ implies $a^{2} = 2\;\mbox{ (mod }3)\;$ in \mathbb{Z}_{3}, a contradiction.
(It can be shown that the equation $x^{2} = 2\;(\mbox{mod}\space p),\;$ where $p\;$ is an odd prime, is solvable if $p = 1, 7 \;(\mbox{mod}\space 8)$ and is unsolvable if $p = 3, 5\space(\mbox{mod}\space 8),$ see [Stark, pp. 311-313].)
In general, it is easy to see that $n^{1/m}$ is irrational if there exists at least one prime $p$ such that $n$ is not a perfect $m^{th}$ power in \mathbb{Z}_{p}.
Proof 14''
This proof was found by Sergey Markelov when yet in high school. In the decimal system, a square of an interger may only end in one of the following digits: $0,1, 4, 5, 6, 9\;$ whereas twice a square may only end with $0,2,8.\;$ Thus assuming $a^2=2b^2,\;$ both $a\;$ and $b\;$ may only end with $0.\;$ This triggers an infinite descent which proves that this is also impossible, as further explained here.
Proof 15
2-proofs-in-1 from The American Mathematical Monthly 114 (May 2007), p. 416. The proof is by Xinyun Zhu of Central Michigan University.
Starting as in the proof from Conway and Guy, let $\sqrt{N}$ is not an integer but a rational number $B/A,$ then
$B/A = NA/B.$
Assume $B/A$ is in lowest terms so that $A$ is minimal. Recollect that $x/y = w/z$ implies
$x/y = (x + tw) / (y + tz),$
for any $t.$
Since $B$ is not divisible by $A,$ there is a $q \gt 0$ satisfying
$0 \lt B - qA \lt A.$
From $B/A = NA/B$ it then follows that
$\sqrt{N} = NA/B = (N\cdot A - qB) / (B - qA)$
which contradicts $B - qA \lt A.$ Alternatively, we may use the fact that for mutually prime $A$ and $B$ there are integer $r$ and s such that $rA + sB = 1.$ Then
$\sqrt{N} = (sN\cdot A + rB) / (sB + rA) = sN\cdot A + rB,$
which is an integer. A contradiction.
Proof 16
(N. C. Ferreño, Yet Another Proof of the Irrationality of $\sqrt{2}$, Am Math Monthly, v 116, n 1 (Jan 2009), pp. 68-69.)
Consider a linear mapping $f:\space\mathbb{R}\rightarrow \mathbb{R}$ given by $f(x) = (\sqrt{2} - 1)x$ as a dynamical system. For each point $x_{0}\in\mathbb{R}$ let us define its orbit $O(x_{0})$ as the sequence of iterates starting at $x_{0},$ namely
$O(x_{0}) = \{(\sqrt{2} - 1)^{n}x:\space n \ge 0\}.$
Since $0 \lt \sqrt{2} - 1 \lt 1,$ it is clear that for each $x_{0}\in \mathbb{R}$ the orbit $O(x_{0})$ converges to zero. Now suppose $\sqrt{2} = p/q$ is a rational number with $p, q \in \mathbb{N}.$ Then, for all $n\in \mathbb{N},$ it holds that
$(\sqrt{2})^{n}q = \begin{cases} 2^{n/2}q, &\mbox{if}\space n \space\mbox{is even}\space\\ 2^{(n-1)/2}p, &\mbox{if}\space n \space\mbox{is odd}\space. \end{cases}$
In either case, $(\sqrt{2})^{n}q$ is a natural number, and from binomial theorem it follows that
$\displaystyle 0 \lt (\sqrt{2} - 1)^{n}q = \sum_{k}\bigg[{n\choose k}\sqrt{2}^{k}(-1)^{n-k}q\bigg]\in\mathbb{Z},$
$k = 1, \ldots, n.$ Therefore $O(x_{0})\subset\mathbb{N}$ which contradicts the fact that $O(x_{0})$ tends to zero.
Proof 17
Yoram Sagher gave a modification of Dedekind's argument (Am Math Monthly, Vol. 95, No. 2. (Feb., 1988), p. 117):
Suppose $\sqrt{k} = m/n,$ where $m$ and $n$ are integers with $n > 0.$ If $k$ is not a square, there is an integer $q$ so that $q < m/n < q + 1.$ Now $m^{2} = kn^{2}$ implies $m(m - qn) = n(kn - qm)$ and, hence, $m/n = (kn - qm)/(m - qn).$ From $q < m/n < q + 1$ we get $0 < m - qn < n.$ Therefore we have:
$\sqrt{k} = (kn - qm)/(m - qn),$
where the denominator is positive and smaller than the one in the original fraction. Continuing, we get an infinite decreasing sequence of positive integers, an impossibility.
This proof does not use any properties of primes and would thus be fully accessible to Pythagoras and to Theodorus.
Proof 17'
Following up on Y. Sagher proof, Robert W. Floyd published (Am Math Monthly, Vol. 96, No. 1 (Jan., 1989), p. 67) an extension:
Assuming Pythagoras understood Euclid's algorithm, the following proofs show how he could have demonstrated that any integer root of an integer is an irrational or an integer, and even that the cube root of an integer either is not the root of a quadratic (i.e., not in the form $(a + b\sqrt{N}) / c$ or is an integer.
I placed the proof into a separate file.
Proof 18
This is a proof by D. Kalman et al (Variations on an Irrational Theme-Geometry, Dynamics, Algebra, Mathematics Magazine, Vol. 70, No. 2 (Apr., 1997), pp. 93-104).
$ABC$ is an isosceles right triangle. $D$ on $AB$ is such that $BD = BC.$ $DE\perp BC;$ $F$ and $G$ are such that $CEGF$ is a square.
$
 $
$
Observe that $CG = DG.$ Indeed, by the construction of $D,$ $\Delta BCD$ is isosceles so that $\angle BDC = \angle BCD.$ Also, $\angle ECG = \angle BDE.$ Subtracting equals from equals, we see that $\angle DCG = \angle CDG,$ implying $CG = CD.$

Let $H$ on $AC$ be such as to form a parallelogram $ADGH.$ Then $\angle FHG = \angle CAB = 45^{\circ}.$ Hence, $\Delta CGH$ is isosceles and $CG = GH.$ But then in the parallelogram $ADGH$ all sides are equal.

The following diagram only shows three equal segments that are important for the proof.

Assume $BC$ and $AB$ are commensurable, i.e. assume that the two have a common unit. Their difference $AD$ is then also wholly measured by the same unit. The unit therefore measures two legs $(GH$ and $CG)$ of the isosceles right $\Delta CGH.$ The unit measures $AC$ and $AH$ and so also $CH.$ We obtain an isosceles right $\Delta CGH$ all of whose sides are measured by the same unit. But $\Delta CGH$ is smaller than $\Delta ABC.$ Since the process could be continued, we obtain a contradiction.
This proof too does not use any properties of primes and would thus be fully accessible to Pythagoras and to Theodorus.
The proof admits an algebraic equivalent. Suppose $e$ is the unit common to $BC$ and $AC:$ $BC = ne$ and $AC = me.$ We then produce successively $AD = (n - m)e,$ $AH = (n - m)e,$ $CH = m - (n - m)e = (2m - n)e;$ and since triangles $ABC$ and $CHG$ are similar, $n/m = (2m - n)/(n - m).$ The latter identity is equivalent to $n^{2} = 2m^{2},$ meaning that $\sqrt{2} = n/m.$ But then also $\sqrt{2} = (2m - n)/(n - m)$ which again leads to an infinite descent. The proof appears to be a geometric equivalent of the short Proof 8.
Proof 19
I am grateful to Aharon Meyerowitz from Florida Atlantic University for bringing to my attention the geometric arguments from The Elements of Dynamic Symmetry by Jay Hambidge (the book is available online.)
Cut off of a $\sqrt{2}\times 1$ rectangle a square of side 1. The rectangle left over will have dimensions $(\sqrt{2} - 1)\times 1.$ Removing from the latter a square as shown in the diagram leaves a rectangle $(\sqrt{2} - 1)\times (2 - \sqrt{2}).$ This rectangle is similar to the one we started with:
$(2 - \sqrt{2}) / (\sqrt{2} - 1) = \sqrt{2} / 1.$
which shows that the standard "infinite descent" argument applies. Were $\sqrt{2}$ rational, it would be possible to select the smallest rectangle with dimensions proportional to $(\sqrt{2} - 1)\times 1.$ As the argument shows, the existence of such a smallest rectangle would lead to a contradiction.
This argument may serve as an illustration to Proof 8.
The book contains another approach illustrated by the following diagram:
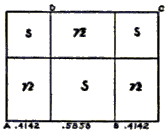
Here two $1\times 1$ squares are drawn at the opposite ends of the rectangle. This splits the original $\sqrt{2}\times 1$ rectangle into one big and two small squares and three rectangles of dimensions $(\sqrt{2} - 1)\times (2 - \sqrt{2}).$ The same argument applies again.
Proof 20
The irrationality of $\sqrt{2}$ is a consequence of the $p$-adic Local-Global Principle. $\sqrt{2}$ is irrational because $2$ is not a quadratic residue modulo $5$!
Proof 21
Also $\sqrt{2}\;$ is irrational because it is represented by an infinite continued fraction. Indeed, $\displaystyle\sqrt{2}+1=2+\frac{1}{\sqrt{2}+1}$ makes it clear that the process of converting $\sqrt{2}+1\;$ into continued fraction never ends, the same holds for $\sqrt{2}.$
Proof 22
The irrationality of $\sqrt{2}$ can be rephrased in a way that appears quite paradoxical: a cover of the unit interval by open intervals centered on rational numbers, with infinite total length does not cover $\sqrt{2}/2$. The details are on a separate page.
Proof 23
A modified argument leads to a criterion of irrationality via a limit. I placed the proof on a separate page.
Proof 24
The concept of limit is central in the following proof that is based on solving a simple difference equation: $x_{n+2}=-2x_{n+1}+x_n,$ where $n=0,1,2,\ldots.$
The details are on a separate page.
Proof 25
Samuel G. Moreno, Esther M. García-Caballero (The Mathematical Gazette, July 2013) derive the irrationality of $\sqrt{2}$ from one of the formulas that accompany a figure in Ramanujan's Notebooks:
The details are in a separate file.
Proof 26
Samuel G. Moreno and Esther M. García-Caballero also proved irrationality of $k$-th roots, for $k\ge 2,$ of integers that are not $k$-th powers. Their proof by induction that employs Bézout's Lemma can be found in a separate file.
Proof 27
Moreno and García-Caballero sent me an unpublished proof where they employed - in a playful manner - the well known formula for the sum of the first odd numbers $\displaystyle n^{2}=\sum_{k=1}^{n}(2k-1);$ this can be found in a separate file.
Proof 28
A purely number theoretical proof - the last for 2014, with a generalization to the irrationality of $\sqrt{a},$ for a square-free $a\in\mathbb{N}.$ Details are in a separate file.
Proof 29
A proof by M. Jacobson and H. Williams exploits the behavior of two sequences defined in terms of each other:
$d_{n+1}=d_n+2s_n,\;d_1=1,\\ s_{n+1}=s_n+d_n,\;s_1=1.$
The details can be found in a separate file.
It's edifying to recall an estimate of approximation of irrational numbers with rational ones.
The irrationality of $\sqrt{2}/2$ leads to an interesting investigation.
In case you are curious, $\sqrt{2}$ is the length of the diagonal of the unit square.
Ludmila Duchêne and Agnès Leblanc put together an enchanting literary tribute to the question of irrationality of $\sqrt{2}$ (in French.)
References
- J-P Allouche & J. Shallit, Automatic Sequences, Cambridge University Press, 2003
- E. Barbin, The Meanings of Mathematical Proof, in In Eves' Circles, J.M.Anthony, ed., MAA, 1994
- J. H. Conway, R. K. Guy, The Book of Numbers, Copernicus, 1996
- P. J. Davis and R. Hersh, The Mathematical Experience, Houghton Mifflin Company, Boston, 1981
- J. W. R. Dedekind, On Irrational Numbers, in A Source Book in Mathematics by D. E. Smith, Dover, 1959, pp. 38-40
- A. De Morgan, On the Study and Difficulties of Mathematics, Dover, 2005, p. 130
- M. Gardner, Gardner's Workout, A K Peters, 2001
- A. Hahn, Basic Calculus: From Archimedes to Newton to its Role in Science, Springer Verlag & Key College, 1998 (Also available online)
- M. Lasckovitch, Conjecture and Proof, MAA, 2001.
- H. Rademacher, O. Toeplitz, The Enjoment of Mathematics, Dover, 1990.
- S. K. Stein, Mathematics: The Man-Made Universe, 3rd edition, Dover, 2000.
- H. M. Stark, An Introduction to Number Theory, MIT Press, 1970
- I. Thomas, Greek Mathematical Works, v1, Harvard University Press, 2006
- D. Wells, You are a Mathematician, John Wiley & Sons, 1995
|Contact| |Front page| |Contents| |Impossible| |Up|
Copyright © 1996-2018 Alexander Bogomolny
73576591
