Geometric Proofs Of the Irrationality of Square Roots
Assuming \(a^{2} = 2b^{2}\), with positive integers \(a\) and \(b\), one can easily establish that also \((2b - a)^{2} = 2(a - b)^{2}\). The impossibility of the former lies in the fact that \(a \gt 2b - a\) (which shows that we are just at the beginning of an infinite descent.) This is one of the proofs of the irrationality of \(\sqrt{2}\). One beautiful illustration of this derivation is due to Stanley Tennenbaum (1927 - 2006) who came up with it in the 1950s:
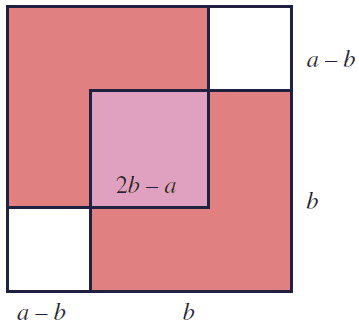
The crucial equality \((2b - a)^{2} = 2(a - b)^{2}\) could be verified by simple algebra; but it also is just a direct consequence of the Carpets Theorem. Such that the illustration falls squarely into the category of proofs without words.
Now, Steven Miller and David Montague found analogues of Tennenbaum's diagram that illustrate the irrationality of \(\sqrt{3}\), \(\sqrt{5}\), \(\sqrt{6}\), and \(\sqrt{n(n+1)/2}\), and invited curious minds to explore further possibilities. Here's the illustration for the square root of 3:
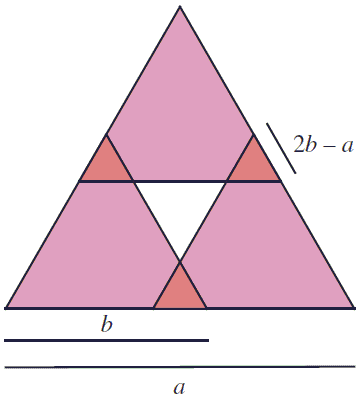
Assuming \(a^{2}=3b^{2}\) and that the sides of the triangles are as shown in the diagram, that of the triangle in the center equals \(2a-3b\) so that Carpets Theorem implies \((2a-3b)^{2}=3(2b-a)^{2}\), implying the possibility of the infinite descent.
For \(a^{2}=6b^{2}\) the diagram is more complex:
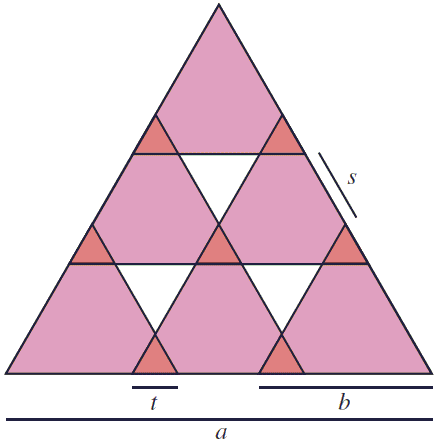
In the diagram, \(t=(3b-a)/2\) and \(s=a-2b\) so that, \(3(a-2b)^{2}=8(\frac{3b-a}{2})^{2}\), because the central triangle of side \(t\) is the intersection of three triangles of side \(b\), so is counted twice. From here we get \(6(a-2b)^{2}=[2(3b-a)]^{2}\), with \(2(3b-a) \lt a\).
To illustrate the irrationality of \(\sqrt{5}\} I prefer the two methods described by E. J. Barbeau. The idea is to find two pentagons whose sides and diagonals are related in an "integral" manner. The first of these (credited to Kurt von Fritz and Wilbur R. Knorr) is illustrated below:
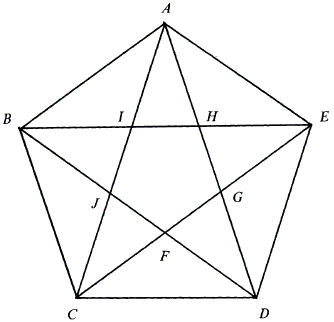
First of all observe that, due to the presence of several kinds of isosceles triangles,
\(IJ = AJ + IC - AC = 2AB - AC\) and
\(IG = AI= AC - IC = AC - AB\).
Setting, \(AB = b\) and \(AC = a\), gives \(2a = (1+\sqrt{5})b\), making incommensurability of \(a\) and \(b\) equivalent to the irrationality of \(\sqrt{5}\). If \(a\) and \(b\) are integers then so are \(b'=IJ = 2b - a\) and \(a'=IG=a-b\) and are related in the same manner while being respectively less than \(b\) and \(a\).
In the case of square (i.e., while proving the irrationality of \(sqrt{2}\)) it is common, for the side of a small square to to be taken equal to the difference of the diagonal and the sides of a larger square. Above, for the pentagon, it was the diagonal of of the smaller figure that was equal to the difference of the diagonal and the sides of a larger one. In the following construction, it's again the side of a small pentagon that is equal to the difference of the diagonal and the sides of the larger pentagon:
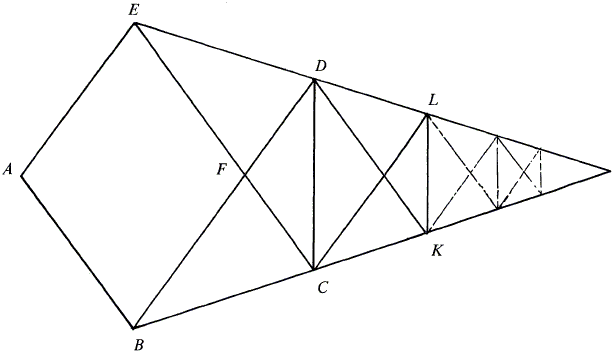
If \(a = BD\), \(b=AB\), \(a'=DC\), and \(b'=CF\), then \(a'=b\) and \(b'=a-b\).
Barbeau also finds a similar illustration for hexagons and also proves that the condition that "the smaller side be the difference of the diagonal and the side of a larger figure" precludes further extension, provided by the "diagonal" one means the "shortest diagonal".
References
- E. J. Barbeau, Incommensurability Proofs: A Pattern That Peters Out, Math. Mag. 56 (1983) 82-90
- S. J. Miller, D. Montague, Picturing Irrationality, Math. Mag. 85 (2012) 110-114
|Contact| |Front page| |Contents| |Up|
Copyright © 1996-2018 Alexander Bogomolny
73579425
