Entry 1.414... in Ramanujan's Notebooks
Samuel G. Moreno, Esther M. García-Caballero
Entry 1 of the unorganised material of Ramanujan's second and third Notebooks (see [Berndt, p. 8]) contains the following figure of a right triangle $ABC,$ in which the two arcs of circles are centred at $B$ and $C.$
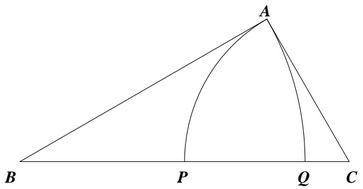
In connection with that figure, Ramanujan gave three formulas, the first one being
(1)
$PQ^{2} = 2BP\cdot QC.$
Our aim is to show that (1) implies the irrationality of $\sqrt{2}.$ (It may be considered as a proof that Ramanujan missed, and this is why we consider that the above-mentioned Entry 1 is more than just 1, so we propose to renumber it as Entry $\sqrt{2}.)$
Suppose $\sqrt{2}=p/q$, where $p$ and $q$ are positive integers and $q$ is the smallest possible. Since $1\lt\sqrt{2}\lt 2,$ then $q\lt p\lt 2q,$ and thus $p = q + k$ for some $k,$ $1\le k \lt q.$ Also, from $p^{2} = 2q^{2},$ we deduce that the triangle with $BC=P=q+k$ and $AB=AC=q$ is the smallest isosceles right-angled triangle with integer sides. For this triangle, equation (1) reads $(q-k)^{2}+2k^{2}.$ This implies that $\sqrt{2}=(q-k)/k,$ where the denominator is positive and smaller than the one in the original fraction. Contradiction.
References
- B. C. Berndt, Ramanujan's Notebooks, Part IV, Springer-Verlag, New York, 1994.
- Samuel G. Moreno, Esther M. García-Caballero, Entry 1.412... in Ramanujan's Notebooks: $\sqrt{2}$ is irrational, The Mathematical Gazette, 97 (2013) 329
|Contact| |Front page| |Contents| |Algebra| |Up|
Copyright © 1996-2018 Alexander Bogomolny73598312
