Problem 1

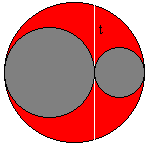
Two smaller circles are outside each other, but inside a third, larger circle. Each of the three circles is tangent to the other two and their centers are along the same straight line. Given r the radius of the larger circle, and t, the piece of the tangent to the two smaller circles at their common point enclosed by the larger circle. Find the area that is inside the larger circle but outside the two smaller ones.

Solution

Let r₁ and r₂ denote the radii of the two small circles. Obviously, r = r₁ + r₂. Also, the chord being perpendicular to the diameter, 2r₁ · 2r₂ = (t/2)². Putting everything together yields the sought area

Finally, S = pt²/8 independent of either r,r₁, or r₂.

Archimedes called one half (upper or lower) of this shape arbelos which literally means "a shoemaker's knife." The property we just proved appears as Proposition 4 in his Book of Lemmas:

The circle in question is circumscribed around a rectangle characteristically formed in an arbelos. (An attempt to present a dynamic proof without words can be found elsewhere.)

Archimedes devoted two more Propositions to the study of arbelos that kept attracting mathematicians through the ensuing centuries. L.Bankoff lists several wonderful properties of arbelos and pertinent bibliography.

The following must be obvious:

(For a generalization of this statement see An Isoperimetric Theorem. See also Chain of Inscribed Circles. The said circles are inscribed in an arbelos.)

---

This applet requires Sun's Java VM 2 which your browser may perceive as a popup. Which it is not. If you want to see the applet work, visit Sun's website at http://www.java.com/en/download/index.jsp, download and install Java VM and enjoy the applet.

---

Reference

1. L. Bankoff, The Marvelous Arbelos, in The Lighter Side of Mathematics, R.K.Guy and R.E.Woodrow, eds, MAA, 1994
2. G. Polya, Mathematical Discovery, John Wiley & Sons, 1981
3. Great Books of The Western World, v. 11, Encyclopaedia Britannica, 1952

On the Web

1. H. P. Boas, Reflections on the Arbelos, a pdf file http://www.math.tamu.edu/~harold.boas/preprints/arbelos.pdf
2. T. Schoch, Arbelos: Amaizing Properties
3. E. W. Weisstein, Arbelos, From MathWorld--A Wolfram Web Resource.
   http://mathworld.wolfram.com/Arbelos.html

• Arbelos - the Shoemaker's Knife
• 7 = 2 + 5 Sangaku
• Another Pair of Twins in Arbelos
• Archimedes' Quadruplets
• Archimedes' Twin Circles and a Brother
• Book of Lemmas: Proposition 5
• Book of Lemmas: Proposition 6
• Chain of Inscribed Circles
• Concurrency in Arbelos
• Concyclic Points in Arbelos
• Ellipse in Arbelos
• Gothic Arc
• Pappus Sangaku
• Rectangle in Arbelos
• Squares in Arbelos
• The Area of Arbelos
• Twin Segments in Arbelos
• Two Arbelos, Two Chains

1. Proposition 1: If two circles touch at A, and if CD, EF be parallel diameters in them, ADF is a straight line.

2. Proposition 2: Let AB be the diameter of a semicircle, and let the tangents to it at B and at any other point D on it meet in T. If now DE be drawn perpendicular to AB, and if AT, DE meet in F, then DF = FE..

3. Proposition 3: Let P be any point on a segment of a circle whose base is AB, and let PN be perpendicular to AB. Take D on AB so that AN = ND. If now PQ be an arc equal to the arc PA, and BQ be joined, then BQ, BD shall be equal.

4. Proposition 4: If AB be the diameter of a semicircle and N any point on AB, and if semicircles be described within the first semicircle and having AN, BN as diameters respectively, the figure included between the circumferences of the three semicircles is "what Archimedes called arbelos"; and its area is equal to the circle on PN as diameter, where PN is perpendicular to AB and meets the original semicircle in P.

5. Proposition 5: Let AB be the diameter of a semicircle, C any point on AB, and CD perpendicular to it, and let semicircles be described within the first semicircle and having AC, CB as diameters. Then if two circles be drawn touching CD on different sides and each touching two of the semicircles, the circles so drawn will be equal.

6. Proposition 6: Let AB, the diameter of a semicircle, be divided at C so that AC = 3/2·CB [or in any ratio]. Describe semicircles within the first semicircle and on AC, CB as diameters, and suppose a circle drawn touching the all three semicircles. If GH be the diameter of this circle, to find relation between GH and AB.

7. Proposition 7: If circles are circumscribed about and inscribed in a square, the circumscribed circle is double of the inscribed square..

8. Proposition 8: If AB be any chord of a circle whose centre is O, and if AB be produced to C so that BC is equal to the radius; if further CO meets the circle in D and be produced to meet the circle the second time in E, the arc AE will be equal to three times the arc BD.

9. Proposition 9: If in a circle two chords AB, CD which do not pass through the centre intersect at right angles, then (arc AD) + (arc CB) = (arc AC) + (arc DB).

10. Proposition 10: Suppose that TA, TB are two tangents to a circle, while TC cuts it. Let BD be the chord through B parallel to TC, and let AD meet TC in E. Then, if EH be drawn perpendicular to BD, it will bisect it in H.

11. Proposition 11: If two chords AB, CD in a circle intersect at right angles in a point O, not being the centre, then AO² + BO² + CO² + DO² = (diameter)².

12. Proposition 12: If AB be the diameter of a semicircle, and TP, TQ the tangents to it from any point T, and if AQ, BP be joined meeting in R, then TR is perpendicular to AB.

13. Proposition 13: If a diameter AB of a circle meet any chord CD, not a diameter, in E, and if AM, BN be drawn perpendicular to CD, then CN = DM.

14. Proposition 14: Let ACB be a semicircle on AB as diameter, and let AD, BE be equal lengths measured along AB from A, B respectively. On AD, BE as diameters describe semicircles on the side towards C, and on DE as diameter a semicircle on the opposite side. Let the perpendicular to AB through O, the centre of the first semicircle, meet the opposite semicircles in C, F respectively. Then shall the area of the figure bounded by the circumferences of all the semicircles be equal to the area of the circle on CF as diameter.

15. Proposition 15: Let AB be the diameter of a circle., AC a side of an inscribed regular pentagon, D the middle point of the arc AC. Join CD and produce it to meet BA produced in E; join AC, DB meeting in F, and Draw FM perpendicular to AB. Then EM = (radius of circle).

|Contact| |Front page| |Contents| |Store| |Geometry| |Up|

Copyright © 1996-2010 Alexander Bogomolny