Salinon: From Archimedes' Book of Lemmas

Proposition II.10 from the second book of Euclid's Elements

If a straight line is bisected, and a straight line is added to it in a straight line, then the square on the whole with the added straight line and the square on the added straight line both together are double the sum of the square on the half and the square described on the straight line made up of the half and the added straight line as on one straight line.

is expressed in modern language concisely as

or, more elegantly (with a = m + n, b = m), as

which is by far more expressive than the original formulation. Interestingly, the proposition is never referred to in the Elements. Why then was it included into this fundamental work? We may only guess. One possibility is that Euclid's mental image of the proposition might have been close to its modern algebraic form, and that Euclid found it satisfactory, if not surprising. (2) might have been illustrated as in the diagram

but negative quantities, like -2ab, at the time of Euclid had yet to wait some 2,000 years to be discovered and accepted. Euclid's original proof is illustrated by an uninspiring diagram

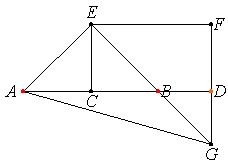
which hardly reminds one of (2), if at all.

Archimedes made use of Proposition II.10 in his Book of Lemmas with a pleasant application:

Proposition 14

Let ACB be a semicircle on AB as diameter, and let AD, BE be equal lengths measured along AB from A, B respectively. On AD, BE as diameters describe semicircles on the side towards C, and on DE as diameter a semicircle on the opposite side. Let the perpendicular to AB through O, the center of the first semicircle, meet the opposite semicircles in C, F respectively.

Then shall the area of the figure bounded by the circumferences of all the semicircles be equal to the area of the circle on CF as diameter.

This applet requires Sun's Java VM 2 which your browser may perceive as a popup. Which it is not. If you want to see the applet work, visit Sun's website at http://www.java.com/en/download/index.jsp, download and install Java VM and enjoy the applet.

Buy this applet What if applet does not run?

Proof

By Eucl.II.10, since ED is bisected at O and produced to A,

EA² + AD² = 2 (EO² + OA²)

and CF = OA + EO = EA. Therefore

AB² + DE² = 4 (EO² + OA²) = 2 (CF² + AD²)

But circles (and therefore semicircles) are to one another as the squares on their radii (or diameters). Therefore

(sum of semicircles on AB, DE) = (circle on CF) + (sum of semicircles on AD, BE).

Therefore

(area of "salinon") = (area of circle on CF as diam.).

Archimedes' proof is short, that of Proposition II.10 from Elements is 5-7 times longer. Archimedes actually derives (2) from Eucl. II.10 in just one step in the form

2 (EO² + OA²) = AE² + AD²   (OA = a, EO = b)

Was he aware of (2)? Given he did not know Algebra, in what sense might have he been? Why did Euclid go to quite a length to prove a statement he never used himself? Was he aware of the nice properties of the salinon? Did Archimedes think of the salinon as an illustration to an algebraic identity, or the other way round? - there is a multitude of questions we shall never have an answer to.

I went through several Greek-English dictionaries to determine the meaning of the word salinon. Unfortunately, none of the available dictionaries contained a matching entry. Close enough appear to be "a vessel for watering mouth", "saliva", and "salt". Taking this with a grain of salt, the first of the possible meanings seems to point to the shape of the figure. If turned upside down, it does resemble a vessel capable of holding water. The second meaning seems to connect with the mouth watering people experience at the sight of a succulent morsel. Under the circumstances, I think it's natural to assume that both Euclid and Archimedes did what they did just because they enjoyed doing it even if it did not seem to offer any immediate payoffs.

Finally note that in the extreme position, when both D and E coincide with O, Proposition 14 confirms one of the properties of Arbelos, symmetric in this case - another of Archimedes' inventions.

Roger Nelsen published a proof without words that reduces the problem of the areas of the regions bounded by circular arcs to that of squares and semisquares. The applet above attempts a hint to Nelsen's proof.

References

1. R. Nelsen, Proof Without Words: The area of a salinon, Mathematics Magazine, 75 (2002), p. 316.

1. Proposition 1: If two circles touch at A, and if CD, EF be parallel diameters in them, ADF is a straight line.

2. Proposition 2: Let AB be the diameter of a semicircle, and let the tangents to it at B and at any other point D on it meet in T. If now DE be drawn perpendicular to AB, and if AT, DE meet in F, then DF = FE..

3. Proposition 3: Let P be any point on a segment of a circle whose base is AB, and let PN be perpendicular to AB. Take D on AB so that AN = ND. If now PQ be an arc equal to the arc PA, and BQ be joined, then BQ, BD shall be equal.

4. Proposition 4: If AB be the diameter of a semicircle and N any point on AB, and if semicircles be described within the first semicircle and having AN, BN as diameters respectively, the figure included between the circumferences of the three semicircles is "what Archimedes called arbelos"; and its area is equal to the circle on PN as diameter, where PN is perpendicular to AB and meets the original semicircle in P.

5. Proposition 5: Let AB be the diameter of a semicircle, C any point on AB, and CD perpendicular to it, and let semicircles be described within the first semicircle and having AC, CB as diameters. Then if two circles be drawn touching CD on different sides and each touching two of the semicircles, the circles so drawn will be equal.

6. Proposition 6: Let AB, the diameter of a semicircle, be divided at C so that AC = 3/2·CB [or in any ratio]. Describe semicircles within the first semicircle and on AC, CB as diameters, and suppose a circle drawn touching the all three semicircles. If GH be the diameter of this circle, to find relation between GH and AB.

7. Proposition 7: If circles are circumscribed about and inscribed in a square, the circumscribed circle is double of the inscribed square..

8. Proposition 8: If AB be any chord of a circle whose centre is O, and if AB be produced to C so that BC is equal to the radius; if further CO meets the circle in D and be produced to meet the circle the second time in E, the arc AE will be equal to three times the arc BD.

9. Proposition 9: If in a circle two chords AB, CD which do not pass through the centre intersect at right angles, then (arc AD) + (arc CB) = (arc AC) + (arc DB).

10. Proposition 10: Suppose that TA, TB are two tangents to a circle, while TC cuts it. Let BD be the chord through B parallel to TC, and let AD meet TC in E. Then, if EH be drawn perpendicular to BD, it will bisect it in H.

11. Proposition 11: If two chords AB, CD in a circle intersect at right angles in a point O, not being the centre, then AO² + BO² + CO² + DO² = (diameter)².

12. Proposition 12: If AB be the diameter of a semicircle, and TP, TQ the tangents to it from any point T, and if AQ, BP be joined meeting in R, then TR is perpendicular to AB.

13. Proposition 13: If a diameter AB of a circle meet any chord CD, not a diameter, in E, and if AM, BN be drawn perpendicular to CD, then CN = DM.

14. Proposition 14: Let ACB be a semicircle on AB as diameter, and let AD, BE be equal lengths measured along AB from A, B respectively. On AD, BE as diameters describe semicircles on the side towards C, and on DE as diameter a semicircle on the opposite side. Let the perpendicular to AB through O, the centre of the first semicircle, meet the opposite semicircles in C, F respectively. Then shall the area of the figure bounded by the circumferences of all the semicircles be equal to the area of the circle on CF as diameter.

15. Proposition 15: Let AB be the diameter of a circle., AC a side of an inscribed regular pentagon, D the middle point of the arc AC. Join CD and produce it to meet BA produced in E; join AC, DB meeting in F, and Draw FM perpendicular to AB. Then EM = (radius of circle).

Reference

1. Great Books of The Western World, v. 11, Encyclopaedia Britannica, 1952

|Contact| |Front page| |Contents| |Geometry| |Up| |Store|

Copyright © 1996-2012 Alexander Bogomolny