Center of Gravity and Motion of Material Points
What is this about?
Problem
Let $A,$ $B,$ $C,$ $D$ be points in a plane and $\lambda$ and $\mu$ two real numbers. Define $E$ and $F$ on $AB$ and $CD$ by $BE/AB=DF/CD=\lambda.$ Define $K$ and $L$ on $AD$ and $BC$ by $DK/AD=BL/BC=\mu.$ Finally, define $G,$ $H,$, $I,$ $M$ - the midpoints of $AC,$ $EF,$ $BD,$ and $KL,$ respectively.
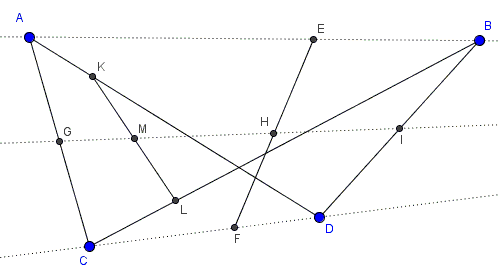
Prove that $G,$ $H,$ $I,$ and $M$ are collinear
Hint
Take a look into center of gravity (barycenter) and barycentric coordinates of material points.
Solution 1
Consider $A,$ $B,$ $C,$ $D$ as material points, placing masses $\lambda$ at $A$ and $C$ and $1-\lambda$ at $B$ and $D.$ Then, with $E=\lambda A + (1-\lambda)B,$ the material point $(E,1)$ is the barycenter of points $(A,\lambda)$ and $(B,1-\lambda).$ Similarly, $(F,1)$ is the barycenter of points $(C,\lambda)$ and $(D,1-\lambda).$ The midpoint $(H,2)=((E+F)/2,2)$ is the barycenter of all four points.
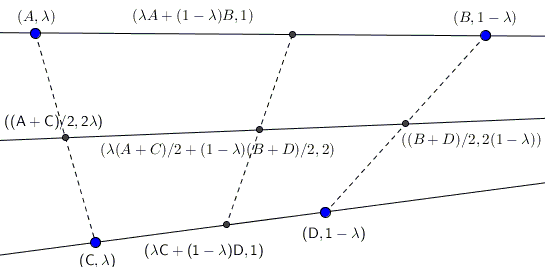
Now, proceed a little differently, first finding $(G,2\lambda)$ and $(I,2(1-\lambda)$ is the barycenters of pairs $(A,\lambda),$ $(C,\lambda)$ and $(B,1-\lambda),$ $(D,1-\lambda).$ Then $(\lambda (A+C)/2 + (1-\lambda)(B+D)/2, 2)$ is the barycenter of all four points and needs to coincide with $(H,2).$ Or, differently, since the barycenter of two points is on the line between these points, the barycenter of the four points $A,$ $B,$ $C,$ $D$ is on the lines $EF$ as well as $GI$ and, hence, at their intersection, implying that $G,$ $H,$ and $I,$ are collinear.
Now, with $\mu$ instead of $\lambda$ find first barycenters of $A$ and $D$ and also of $B$ and $C$ and then combine the two into the barycenter of all four points, with the same result as above. This will show that $M$ is collinear with $G$ and $I$ and, therefore, also with $H.$
Solution 2
The parametric equations of lines $AB$ and $CD$ are, respectively, $f(t)=A+t\mathbf{AB}$ and $g(t)=C+t\mathbf{CD},$ where the two vectors are in bold (e.g., $\mathbf{AB}=B-A)$ and $t$ is a real parameter such that $f(0)=A,$ $f(1)=B,$ $g(0)=C,$ $g(1)=D.$ The function $h=(f+g)/2$ is also linear such that $h(0)=G$ and $h(1)=I.$ Furthermore, for any $t,$ $h(t)$ is the midpoint between $f(t)$and $g(t),$ as well as being on the line between $h(0)$ and $h(1).$ The given problem corresponds to choosing $t=1-\lambda.$
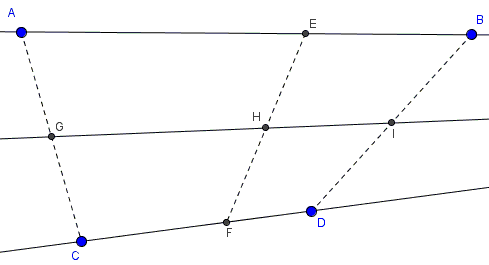
The derivation for point $M$ is analogous.
We may imagine one traveler walking along $AB$ and another along $CD$ with constant speeds such that they are at $A$ and $C$ at time $t=0$ and at $B$ and $D$ at time $T=1.$ If there is an elastic band stretched between them, its midpoint will also move along a straight line with a fixed speed.
Finally, note that, instead of talking of a midpoint, we could have chosen any fixed ratio $r$ and points it defines between the pairs $A,$ $C$ and $B,$ $D.$
Acknowledgment
The problem has been posted by Dao Thanh Oai at the CutTheKnotMath facebook page.
This is a clear generalization of a property of bimedians and Newton's line in a quadrilateral.
Finally, the statement is actually a reformulation of Hjelmslev's Theorem.
Barycenter and Barycentric Coordinates
- 3D Quadrilateral - a Coffin Problem
- Barycentric Coordinates
- Barycentric Coordinates: a Tool
- Barycentric Coordinates and Geometric Probability
- Ceva's Theorem
- Determinants, Area, and Barycentric Coordinates
- Maxwell Theorem via the Center of Gravity
- Bimedians in a Quadrilateral
- Simultaneous Generalization of the Theorems of Ceva and Menelaus
- Three glasses puzzle
- Van Obel Theorem and Barycentric Coordinates
- 1961 IMO, Problem 4. An exercise in barycentric coordinates
- Centroids in Polygon
- Center of Gravity and Motion of Material Points
- Isotomic Reciprocity
- An Affine Property of Barycenter
- Problem in Direct Similarity
- Circles in Barycentric Coordinates
- Barycenter of Cevian Triangle
- Concurrent Chords in a Circle, Equally Inclined
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny71573633
