Hjelmslev's Theorem:
What is this about?
A Mathematical Droodle

(The black segments in the applet can be dragged by their end points or by any interior point.)

The applet illustrates what's known as Hjelmslev's theorem, named after the notable Danish mathematician Johannes Hjelmslev (1873-1950):

If two line segments $I_{1}$ and $I_{2}$ are related by an isometry $f: P_{1} \rightarrow P_{2},$ then the midpoints between the corresponding points $P_{1},$ $P_{2}$ are either all different and collinear or all coincide.

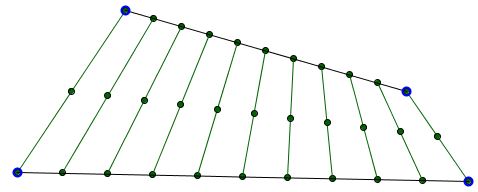
Hjelmslev's theorem

The applet in fact shows more: the relation between the two segments need not be isometric, it may be just affine. Also, it is not necessary to consider the midpoints of $P_{1}P_{2}.$ All the points that are determined by the same linear combination of the corresponding points are either different and collinear or all coincide.

Points in a segment $AB$ are parametrized by a linear expression:

$P = P(t) = tA + (1 - t)B,$

where $0 \le t \le 1.$ If $A$ and $B$ are different, $P(t)$ is 1-1, for

$\begin{align} P(t) - P(s) &= (t - s)A + (s - t)B\\ &= (t - s)(A - B). \end{align}$

Thus $P(s) = P(t)$ implies either $t = s$ or $A = B.$

A mapping $f$ defined on such a segment $AB$ is affine provided

$f(tA + (1 - t)B) = tf(A) + (1 - t)f(B).$

For two segments $A_{1}B_{1},$ $A_{2}B_{2},$ an affine mapping $f$ is defined by

$f(P_{1}) = f(tA_{1} + (1 - t)B_{1}) = tA_{2} + (1 - t)B_{2} = P_{2}.$

For a fixed $r,$ $0 \le r \le 1,$ point $P = rP_{1} + (1 - r)P_{2}$ lies on the segment $P_{1}P_{2}.$ Further,

(1)

$\begin{align} P &= rP_{1} + (1 - r)P_{2}\\ &= r[tA_{1} + (1 - t)B_{1}] + (1 - r)[tA_{2} + (1 - t)B_{2}]\\ &= t[rA_{1} + (1 - r)A_{2}] + (1 - t)[rB_{1} + (1 - r)B_{2}]\\ &= tA_{r} + (1 - t)B_{r} \end{align}$

and therefore belongs to the segment joining

$A_{r} = rA_{1} + (1 - r)A_{2}$

with

$B_{r} = rB_{1} + (1 - r)B_{2},$

provided of course the two are different. If they are not, all the linear combinations in (1) coincide. For $r = 1/2,$ we obtain the Hjelmslev's Theorem.

(A JavaScript illustration is available elsewhere.)

References

H. S. M. Coxeter, Introduction to Geometry, John Wiley & Sons, 1961

72104495

Hjelmslev's Theorem:What is this about? A Mathematical Droodle

References

Hjelmslev's Theorem:
What is this about?
A Mathematical Droodle