What Is Area?
- What Is Area
- Elementary Introduction into the Concept of Area
- Equidecomposition of a Triangle and a Rectangle: first variant
- Pick's Theorem
- Area of a Circle by Rabbi Abraham bar Hiyya Hanasi
- Area of a Circle by Leonardo da Vinci
- Volume and Area of Torricelli's Trumpet
Area, as many other mathematical concepts, has experiential origins. Intuitively, this is the measure of expanse associated with plane figures. Area is a \(2\)-dimensional analogue of the \(1\)-dimensional length and \(3\)-dimensional volume.
Paint containers carry a mention of the area the paint should suffice to cover. Area of a forest region is an indicator of the number of trees that grow there, and vice versa.
As many other mathematical concepts, area can be defined in a veriety of ways. The context and potential applications may dictate which of the possible definitions is preferable under given circumstances.
In general, the three commonplace terms length, area, and volume relate to three instances of a general concept of measure. A measure \(M\) is a non-negative
- \(M(A) \ge 0.\)
- \(M(\cup_{n=1}^{\infty}A_{n}) = \sum_{n=1}^{\infty}M(A_{n})\), for all families of pairwise disjoint sets \(A_{n}.\)
Measures are constructed starting with an assignment of values to some basic sets. For example, in the linear (\(1\)-dimensional) case, all segments \((a, b), [a, b), (a, b], [a, b], a < b,\) may be assigned the value \(b - a\). Next, the disjoint unions of open segments \((a_{n}, b_{n}), n = 1, 2, ...\) are assigned the value of \(\sum_{n=1}^{\infty}(b_{n}-a_{n})\), and similarly for the unions of semi-open intervals. Every linear set \(A\) admits a cover by countably many semi-open intervals \([a_{n}, b_{n}), n = 1, 2, ...\). The values \(\sum_{n=1}^{\infty}(b_{n}-a_{n})\) of all such covers, being non-negative, are bounded from below which allows one to assign the value of \(\inf(\sum_{n=1}^{\infty}(b_{n}-a_{n}))\) to the set \(A\). This, however, does not define a measure yet, but what is known as the outer measure \(M_{e}\). In this manner, all linear sets A are assigned an outer measure.
So defined outer measure is non-negative, monotone and subadditive:
- \(M(A) \ge 0.\)
- \(A\subset B\) implies \(M_{e}(A) \le M_{e}(B).\)
- \(M(\cup_{n=1}^{\infty}A_{n}) ≤ \sum_{n=1}^{\infty}M(A_{n}).\)
Not all sets are created equal. A set is called (Carathéodory) measurable if \(M_{e}(A∩E) + M_{e}(E-A) = M_{e}(E)\) for every set \(E\). Measurable sets form a \(\sigma\)-algebra on which the outer measure has the two required properties of measure.
In a similar manner, one may define the Hausdorff (outer) measure \(H^{s}, s > 0,\) by setting \(H^{s}([a, b)) = (b-a)^{s}.\) (In passing, the Hausdorff dimension of set A is defined as a real number \(s_{0}\) such that \(H^{s}(A) = \infty,\) for \(s < s_{0}\) and \(H^{s}(A) = 0,\) for \(s > s_{0}\).)
The Dirac measure assign values 1 to points in a discrete set, say the set of natural numbers \(Z\), and to each interval the number of points from that descrete that.
In the \(2\)-dimensional case, an \(a\times b\) rectangle is usually assinged a value of \(a\cdot b\) and the construction analogous to the above leads to the measure that generalizes the concept of area. As you can see (or just sense, because I omitted all the proofs) the mathematical notion of area as a full pledged measure is not at all simple.
However, for polygonal shapes, the process of assigning areas could be simplified based on the idea of equidecomposition:
Two shapes are equidecomposable, provided one could be cut into a finite number of pieces that can be rearranged to form the second shape without overlap.
Formally, we shall define area as a non-negative finitely additive function \(S\) taking the same values for all congruent shapes:
- \(S(A) \ge 0.\)
- \(S(\cup_{n=1}^{N}A_{n}) = \sum_{n=1}^{N}S(A_{n})\), for all families of pairwise disjoint sets \(A_{n}, n = 1, 2, ..., N.\)
- \(A = B\) implies \(S(A) = S(B).\)
(Here, disjoint sets may share parts of their boundaries but not interior points.)
There is a number of ways to construct such a function. Each proceeds in several steps starting with a chosen basic figure. [Euclid I.35-I.38, Kiselev, Ch. 5, Hadamard, Book IV, and Jacobs, Ch. 9] choose rectangle as the basic figure, defining its area (Euclid only implicitly) as the product of its sides. [Hilbert, Ch. IV] starts with triangle and defines its area as half the product of a base and the corresponding altitude. The fact that this definition is independent of which side is perceived as a base follows from the similarity of right triangles \(ADC\) and \(BEC\) in the following diagram:

The similarity of the two triangles gives a proportion \(AC/BC = AD/BE\) which is the same as \(BC\cdot AD = AC\cdot BE.\) Clearly, bringing in the third side would give the same product. The area of a triangle is uniquely defined as half that (or either) product. As a consequence, the area of a rectangle is the product of two sides; the area of parallelogram is the product of either base times the corresponding altitude.
Were we to start with a rectangle, the finite addivity property would make it necessary to define the area of a triangle as half that of one of the associated rectangles and then prove independence of the result on the choice of the rectangle.
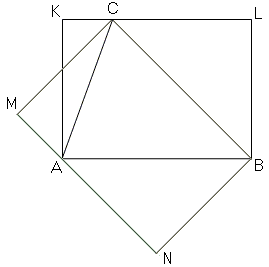
By Euclid I.37-38, the area of \(\Delta ABC\) is half that of rectangle \(ABLK\) and also that of \(BCMN\). But this exactly means that the products of the sides of the two rectangles are the same. (As an exercise, find a decomposition of one of the rectangles into triangles that, when rearranged, form the other rectangle.)
To define the area of a polygon \(P\) triangulate it into the union of non-overlapping triangles \(\{T_{n}\}\) and declare the sum of their areas as that of \(P\). This definition is independent of triangulation. For another triangulation \(\{U_{n}\}\) of \(P\), form all possible intersection \(\{T_{k}\cap U_{m}\}\). Each of this (if not empty) is a polygon which, if not in itself a triangle, could be triangulated. Thus we find that both families of triangles \(\{T_{n}\}\) and \(\{U_{m}\}\) are composed of the same triangular pieces and define, therefore, the same area.
Finite additivity implies monotonicity of area: \(A\subset B\) implies \(S(A) \le S(B),\) for polygonal A and B. The adopted formula for the area of rectangles and triangles leads to the well known formulas of other shapes, trapezoids in particular. It also implies continuity: if two polygons are close (e.g., in the sense of the Hausdorff distance) then their areas are also close. Continuity, in turn makes it possible to define area for curvilinear shapes. For example, the area of a circle is defined as the common limit of the areas of inscribed and circumscribed regular polygons.
References
- J. Hadamard, Leçons de géométrie élémentaire, tome I, 13e édition, 1947, Editions Jacques Gabay, 1988, ISBN 2-87647-038-1.
- D. Hilbert, Foundations of Geometry, Open Court, 1999
- H. R. Jacobs, Geometry, 3rd edition, W. H. Freeman and Company, 2003
- Kiselev's Geometry. Book I. PLANIMETRY, adapted from Russian by Alexander Givental, Sumizdat, 2006.
|Contact| |Front page| |Contents| |Algebra| |Up|
Copyright © 1996-2018 Alexander Bogomolny
71536958
