The many ways to construct a triangle III

A, h_b, h_c

A right triangle is well defined by a leg and an angle. Therefore, starting with an angle A, we may first construct triangle AH_cC to obtain vertex C, and, in a similar manner, the triangle AH_bB to obtain vertex B.

A, a, h_a

Construct an arc (part of a circle) subtending segment BC = a such that for every point A on it, angle BAC equals the given angle A. Draw a line parallel to BC at the distance h_a. There could be 0,1, or 2 points of intersection of the line with the arc. In the latter case solutions are mirror images of each other; so even then there is at most one solution.

h_a, h_b, h_c

Since S = 2ah_a = 2bh_b = 2ch_c, a:b:c = 1/h_a = 1/h_b = 1/h_c. Since the heights are given, we may construct a triangle similar to the sought one. Consider in thus constructed triangle one altitude, say, h_a' and apply similarity transformation with the ratio h_a/h_a'.

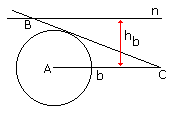
h_a, h_b, b

Let AC has length b. Draw a line n parallel to AC at the distance of h_b. Draw a circle with center at A and radius h_a. Let B be the intersection if line n with the tangent to the circle drawn from C.

a, h_b, m_b

First, construct a right triangle BCH_b with a side a and hypotenuse h_b. Extend CH_b beyond H_b. From B sweep and arc of radius m_b. Let M₁ and M₂ be the points of intersection of the arc and the line CH_b. Several cases are possible. If m_b is too short to reach the line, there is no solutions. If m_b = h_b, there is a single solution and the triangle is isosceles. When M₁ and M₂ exist and are distinct, still there are two solutions corresponding to M₁ and M₂. If M₁ is on the other side of C than H_b, then h_b has its foot outside the triangle ABC.

R, a, b

Draw a circle of radius R and, in it, two chords that share an end.

h_a, h_b, m_a

a, h_a, m_a

Construct ΔAM_aH_a. Line M_aH_a determines the base of the triangle whose middle point coincides with M_a. From M_a measure a/2 in both directions to obtain points B and C.

Another construction (Jacopo D'Aurizio): Draw a line parallel to a at distance h_a, then intersect it with a circle centered in the midpoint of a having radius equal to m_a.

a, b, l_c

With the center C draw three circles of radii a, b, and l_c. For the simplicity sake, the circles will be denoted by their radii: circle a, circle b, and circle l_c. We are looking for a segment AB (with A on circle b and B on circle a) that is cut by circle l_c in the ratio a/b (recollect one of the basic properties of angular bisectors.)

Let B be an arbitrary point on circle a. Perform homothety (central similarity transformation) with center B and coefficient of similarity a/(a+b) on circle b. We'll get the blue circle with radius a'. The blue circle intersects circle l_c at point L_c (and, generally, at a second point.) Draw the line BL_c and continue it beyond L_c to the intersection with the circle b at point A.

Note that, since L_c is collinear with A and B and lies on the blue circle, point L_c is the image of point A under the homothety. It follows that BL_c/BA = a/(a+b). But then L_cA/BA = b/(a+b), so that BL_c/L_cA = a/b. Having this property of L_c in mind we can prove that ΔABC solves our problem.

Indeed, its two sides AC and BC have the given lengths b and a, respectively. Segment CL_c has the length l_c, and the only thing we have to show is that CL_c is the bisector of angle C. We know that, for the bisector, the point L_c divides the side AB in the ratio a/b. Since, on AB, there is only one such point, the point defines the bisector uniquely. But, as we have seen, our point L_c has exactly that property. Therefore, by construction, the line CL_c is indeed the bisector of angle C.

A, B, l_c

Two angles uniquely define a family of similar triangles. Construct any member of the family. Draw the angle bisector l_c. If it's of right length, we are finished. Otherwise, the ratio of this bisector to the given one defines the coefficient of proportionality to apply to our triangle in order to get a similar one in which the bisector l_c is of right length.

A, h_a, p

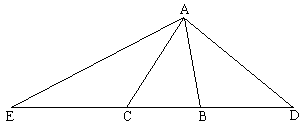
Assume we managed to construct ΔABC. Extend BC to DE adding BD = AB and CE = AC. Thus DE = p. Both ΔABD and ΔACE are isosceles. From here, ∠EAC = ∠ACB/2 and ∠DAB = ∠ABC/2. Summing up, ∠DAE = A/2 + 90°.

A, R, r

A, O, H

(By jack202.) If we know the position of A, O, H in a triangle we can trace

1. The circumcircle D (center O) and radius OA

2. The 9-point circle E (the center is the midpoint of OH, the circle passes trough the midpoint of AH, or has the radius which half that of D.)

The line through A and H intersects E in a point (F) that is the feet of the altitude AH. Now trace the perpendicular r to AH trough F. It will intersect D at the vertices B and C.