The Medians
Below I offer a proof to the well known
Theorem
Three medians of a triangle meet at a point - centroid of the triangle.
The proof is due to Rosemary Ramsey, a graduate student at the University of Chicago; it is based on the following
Lemma
The medians of a triangle serve as the medians of its medial triangle.
Proof of Lemma
Let MMa, MMb, MMc be the three medians of ΔABC such that MaMbMb is its medial triangle. I'll prove that MMa is also a median of ΔMaMbMc.
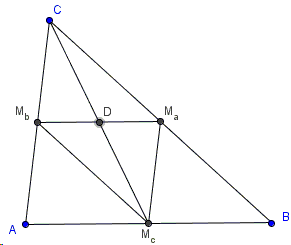
The midlines in a triangle are parallel to the corresponding sides, in particular, MbMc||BC and MaMc||AC, implying that the quadrilateral CMbMcMa is parallelogram. In a parallelogram the diagonals are divided into halves by their point of intersection, D in the above diagram. Therefore, McD is a median of ΔMaMbMc.
In addition, we may observe that the medial lines cut a triangle into four smaller ones, all equal, such that the area of each is 1/4 of the area of the reference triangle.
Proof of Theorem
Assume to the contrary that the medians in a triangle are not concurrent:
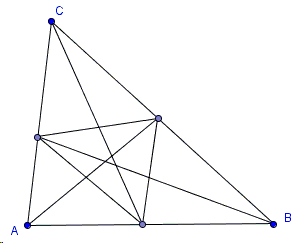
Their three points of intersection form a triangle, say, ΔDEF which is located entirely within (i.e., in the interior) of ΔABC. This implies that the area ΔDEF is less than that of ΔABC. Observe that, by our assumption, the area of ΔDEF could not be zero, for that would imply that it's degenerate. However, if the three points of intersection of the medians are collinear some two intersect on the third, meaning that the three are concurrent.
By Lemma, the medians of the medial triangle ΔMaMbMc are those of ΔABC. Thus we can iterate: the medians of ΔMaMbMc form (the same) ΔDEF which lies entirely within ΔMaMbMc and so its area is less than that of ΔMaMbMc. But the latter is just 1/4 of the area of ΔABC. Repeating the steps leads to
Area(ΔDEF) < 4-n·Area(ΔABC),
for any positive integer n, implying that Area(ΔDEF) = 0. But a nondegenerate triangle has positive area; and we are done.
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
73571826
