Seven Problems in Equilateral Triangle
Solution to Problem 4

Given an equilateral triangle $ABC$ with the base extended to twice its length: $AB'=AB.$ Let $B'I$ (with $I$ on $(ABC))$ be the second tangent from $B'$ to the incircle of $\Delta ABC;$ $L$ the intersection of $B'I$ with $(ABC).$ $CL$ intersects $B'B$ in $J$ and $B'F$ in $K.$

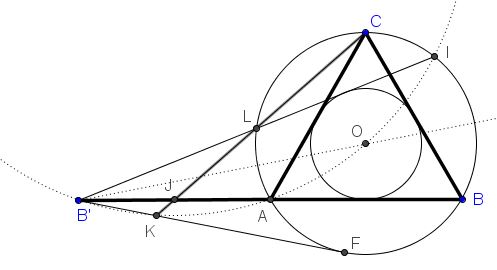
Problem 4 in equilateral triangle with one side extanded

Prove that

$B'J=JA,$
$K$ is concyclic with $B',A,O,I.$

Solution

Observe that, since $AB'=AB,$ due to symmetry in $B'O,$ where $O$ is the center/circumcenter of $\Delta ABC,$ $B'L=LI.$

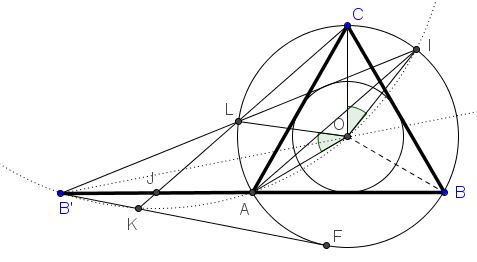
Problem 4 in equilateral triangle with one side extanded, solution

Next, let's show that $CL\parallel IA.$ Indeed, as has been shown, points $B',A,O,I$ are concyclic so that, in particular $\angle IB'A + \angle IOA = 180^{\circ}.$ On the other hand, $\angle IB'A=\frac{1}{2}(\overparen{BI}-\overparen{AL}).$ So we have

$\begin{align} 180^{\circ} &= \angle IB'A + \angle IOA\\ &=\frac{1}{2}(\overparen{BI}-\overparen{AL})+(240^{\circ}-\overparen{BI})\\ &=240^{\circ}-\frac{1}{2}(\overparen{AL}+\overparen{BI})\\ &=240^{\circ}-\frac{1}{2}\overparen{AL}-\frac{1}{2}(120^{\circ}-\overparen{IC})\\ &=180^{\circ}-\frac{1}{2}\overparen{AL}+\frac{1}{2}\overparen{IC}, \end{align}$

implying $\overparen{AL}=\overparen{IC}$ which makes $CL\parallel IA.$ By one of Thales' theorems and since $B'L=LI,$ $B'J=JA.$

For the next step, let's study the clockwise rotation around $O$ through $120^{\circ}.$

Problem 4 in equilateral triangle with one side extanded, solution, step 2

First, by construction, $\angle B'AO=150^{\circ}$ so that $\overparen{B'AO}=360^{\circ}-2\cdot 150^{\circ}=60^{\circ}.$ It follows that $B'O$ is a side of the regular hexagon inscribed into circle $(B'AOI)$ and, as a consequence, it forms a $120^{\circ}$ angle with the adjacent side of the hexagon. In other words, the image of $B'O$ under the said rotation is a chord of the circle $(B'AOI).$ Let it be $A'O:$ $\angle B'OA'=120^{\circ}$ and $B'O=A'O.$

For convenience, let's have a notation for this rotation: $\mathcal{R}.$ So, we found that if $A'=\mathcal{R} (B')$ then $A'$ lies on $(B'AOI)$ and $\angle B'OA'=120^{\circ}$.

Further, $\mathcal{R} (AB)=CA,$ implying $\mathcal{R} (BB')=AA',$ so that $AC$ extended twice to its length ends up at $A'.$ $\mathcal{R} (B'F)=A'V,$ tangent to $(ABC)$ with $V$ on $(ABC).$ Form here, $\angle (VA',B'F)=60^{\circ}.$

$\mathcal{R} (CK)=BK',$ with $K'$ on $A'V.$ (Also, $\mathcal{R} (L)=I$ because $\angle AOC=\angle LOI$ by the first part of the proof.)

If $\overline{K}$ is the second intersection of $A'V$ with $(B'AOI)$ then $\angle AA'\overline{K}=\angle BB'F;$ this implies that $B'F$ crosses $(B'AOI)$ in $\overline{K}.$ (Otherwise, there would be two equal inscribed angles subtended by arcs of different lengths.) Both points, $K$ and $\overline{K}$ lie on $B'F,$ $\overline{K}$ is also on $(B'AOI)$. It remains to be shown that the two points coincide.

Now that we found the intersection of $A'V$ and $B'F$ to be $\overline{K},$ we can claim that $\angle A'\overline{K}F=\angle V\overline{K}F=\angle (VA',B'F)=60^{\circ},$ making $\Delta \overline{K}FV$ equilateral. And, since $\angle F\overline{K}V$ is half the difference of the two arcs $VF,$ the short one is $120^{\circ},$ from which $VF=BC:$ the two equilateral triangles are equal.

Let $Q$ be the center of $(B'AOI).$ $AI$ is the common chord of $(B'AOI)$ and $(ABC$) and, as such, is perpendicular to the line of centers $OQ.$ In addition, $L$ and $C$ are symmetric in $OQ$ as are $B'$ and $A'.$

Let $\mathcal{O}(X)$ denote the power of a point $X$ with respect to $(ABC),$ and $\mathcal{Q}(X)$ that with respect to $(B'AOI).$ Note that $\mathcal{O}(\overline{K})=(\overline{K}F)^{2}=(AB)^{2}$ and $\mathcal{Q}(\overline{K})=0.$ For $J,$ due to the first part of the proof, $\mathcal{Q}(J)=B'J\cdot AJ=(AB)^{2}/4,$ whereas $\mathcal{O}(J)=AJ\cdot BJ=3(AB)^{2}/4.$ It follows that

$\mathcal{O}(\overline{K})-\mathcal{O}(J)=\displaystyle\frac{(AB)^{2}}{4}=\mathcal{Q}(\overline{K})-\mathcal{Q}(J).$

It follows that $J\overline{K}$ is parallel to the radical axis of the two circles $(O)$ and $(Q)$ which is $AI.$ But we previously found that $AI\parallel CL,$ i.e., $AI\parallel CJ.$ Thus we conclude that $\overline{K}$ lies on exactly same straight line as $K$ and, since they both also lie on $B'F,$ they coincide.

Acknowledgment

The proof is an expanded (probably, unnecessarily) version of the one posted by Machó Bónis at the CutTheKnotMath facebook page.

71544768

Seven Problems in Equilateral Triangle Solution to Problem 4

Solution

Acknowledgment

Seven Problems in Equilateral Triangle
Solution to Problem 4