Seven Problems in Equilateral Triangle
Solution to Problem 3

Given an equilateral triangle $ABC$ with the base extended to twice its length: $AB'=AB.$ Let $B'I$ (with $I$ on $(ABC))$ be the second tangent from $B'$ to the incircle of $\Delta ABC.$

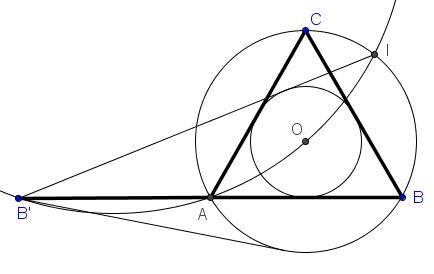
Problem 3 in equilateral triangle with one side extanded

Prove that four points $B',$ $A,$ $O,$ and $I$ are concyclic.

Solution

The problem is easily solved by angle chasing.

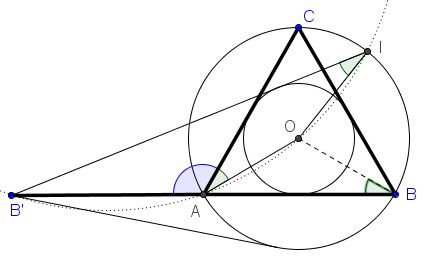
Problem 3 in equilateral triangle with one side extanded, solution

We know that $\angle B'IO=30^{\circ}.$ Obviously, $\angle B'AO=150^{\circ},$ implying that $\angle B'IO+\angle B'AO=180^{\circ}$ which makes quadrilateral $B'AOI$ cyclic.

Acknowledgment

The proof has been suggested by Machó Bónis at the CutTheKnotMath facebook page.

71545951

Seven Problems in Equilateral Triangle Solution to Problem 3

Solution

Acknowledgment

Seven Problems in Equilateral Triangle
Solution to Problem 3