Thales' Theorems
There are several theorems that are attributed to Thales of Miletus (c. 620 - c. 546 BC), the first of the Seven Sages of Ancient Greece (Plato, Protagoras.)
The most commented on is the one that later became known as Pons Asinorum (Euclid I.5):
In isosceles triangles the angles at the base equal one another, and, if the equal straight lines are produced further, then the angles under the base equal one another.
Sir Thomas L. Heath in his commentary on Euclid I notes that Aristotle (384 - 322 BC) was familiar with the statement and proofs different from Euclid's. The one which is related with other Thales' propositions asserts that the angles between a chord and a circle at the two ends of the chord are equal. Both Pappus (c. 290 - c. 350 AD) and Proclus (412 - 485 AD) supplied additional proofs.
Besides Pons Asinorum, Proclus list four statements authored by Thales (his comments accompany each of the statements):
The circle is bisected by its diameter.
They say that Thales was the first to demonstrate that the circle is bisected by its diameter, the cause of the bisection being the unimpeded passage of the straight line through the center.
The vertical and opposite angles are equal.
This theorem, that when two straight lines cut one another the vertical and opposite angles are equal, was first discovered, as Eudemus says, by Thales, though the scientific demonstration was improved by the writer of the Elements.
Equality of triangles (by two angles and a side).
Eudemus in his History of Geometry attributes this theorem to Thales. For he says that the method by which Thales showed how to find the distance of the ships at sea necessarily involves this method.
Heath comments that most likely "the observer had a rough instrument made of a straight stick and a cross-piece fastened to it so as to be capable of turning about the fastening in such a manner so that it could form any angle with the stick and would remain where it was put. The observer, standing on the top of a tower or some other eminence on the shore, would fix the stick in the upright position and direct the cross-pieces towards the ship. Leaving the cross-piece at this angle, he would turn the stick around, keeping it vertical, until the cross-piece pointed to come object on the land, which would be noted. The distance between the foot of the tower and this object would, by Euclid I.26, be equal to the distance of the ship."
The angle in a semi-circle is right angle.
Pamphilia says that, having learnt geometry from the Egyptians, he was the first to inscribe in a circle a right-angled triangle, whereupon he sacrificed an ox. Others say it was Pythagoras, among them being Apollodorus the calculator.
![]()
The latter theorem is dealt with elsewhere. But the one theorem that is most often referred to as Thales' does not appear to have been mentioned by Proclus. This is the most useful one that is also known as the Intercept theorem. It to is also dealt with on a special page.
The theorem is the subject of Euclid VI.2:
If a straight line is drawn parallel to one of the sides of a triangle, then it cuts the other sides of the triangle, or these produced, proportionally; and, if the sides of the triangle, or the sides produced, are cut proportionally, then the line joining the points of section is parallel to the remaining side of the triangle.
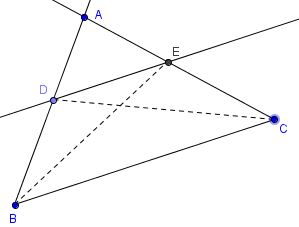
Coxeter points out useful corollaries from Pons Asinorum:
(III.3) If a straight line passing through the center of a circle bisects a straight line not passing through the center, then it also cuts it at right angles; and if it cuts it at right angles, then it also bisects it.
(III.20) In a circle the angle at the center is double the angle at the circumference when the angles have the same circumference as base.
(III.21) In a circle the angles in the same segment equal one another.
(III.22) The sum of the opposite angles of quadrilaterals in circles equals two right angles.
(III.32) If a straight line touches a circle, and from the point of contact there is drawn across, in the circle, a straight line cutting the circle, then the angles which it makes with the tangent equal the angles in the alternate segments of the circle.
References
- H. S. M. Coxeter, Introduction to Geometry, John Wiley & Sons, 1961
- T. L. Heath, Euclid: The Thirteen Books of The Elements, Dover, 1956
- I. Thomas, Greek Mathematical Works, v. 1, Harvard University Press, 2006, 165-169
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73452946
