Solution VII by Vo Duc Dien

Triangles with Equal Area VII

Here is Problem 4 from the IMO 2007:

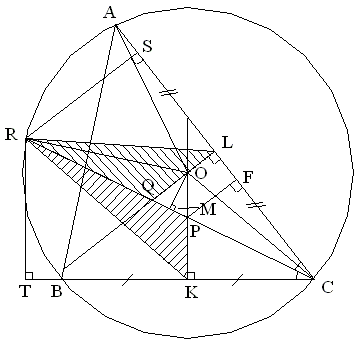
In triangle ABC the bisector of angle BCA intersects the circumcircle again at R, the perpendicular bisector of BC at P, and the perpendicular bisector of AC at Q. The midpoint of BC is K and the midpoint of AC is L. Prove that the triangles RPK and RQL have the same area.

The solution below is by Vo Duc Dien.

problem #4 from 2007 IMO, solution by Vo Duc Dien

From R draw two lines perpendicular to BC and AC meeting them at T and S, respectively. Also, let the perpendicular from P to AC meet AC at F.

To prove that the two triangles RPK and RQL have the same area suffice it to show that

(1)	TK×PK = SL×QL.

Since CR is the bisector of ∠ACB, ΔKPC = ΔFPC and, similarly, ΔTRC = ΔSRC. Thus TK = SF and PK = PF, implying that (1) is equivalent to PF×SF = SL×QL, or

(2)	PF / QL = SL / SF.

But SL / SF = RQ / RP (since the three lines RS, QL, and PF are parallel), so that (2) is equivalent to PF / QL = RQ / RP, or

(3)	QL / PF = RP / RQ

Also note that QL / PF = QC / PC, implying that (3) is equivalent to

(4)	QC / PC = RP / RQ.

Now, QC = QP + PC and RP = RQ + QP which reduces (4) to 1 + QP / PC = 1 + QP / RQ, or simply to

(5)

PC = RQ.

Thus (5) is equivalent to (1) such that proving (5) solves the problem.

Note that O is the circumcenter of ΔABC. Let M be the foot of the perpendicular from O to RC.

Angles MOP and PCK that have perpendicular sides are equal, and for the same reason ∠MOQ = ∠PCF. Since ∠PCK = ∠PCF, angles MOP and MOQ are equal, making triangles MOP and MOQ congruent, wherefrom

(6)

OQ = OP.

Note that

(7) OR = OC

(since R is on the circumcircle of ΔABC with the circumcenter O). This makes ΔCOR isosceles. In particular, ∠ROM = ∠COM and then also

(8)	∠ROQ = ∠COP.

From (6)-(8), ΔROQ = ΔCOP and, finally, PC = RQ which is exactly (5), the condition we set out to prove.

2007 IMO, Problem 4

72104041