Triangles with Equal Area V
Here is Problem 4 from the IMO 2007:
| |
In triangle ABC the bisector of angle BCA intersects the circumcircle again at R, the perpendicular bisector of BC at P, and the perpendicular bisector of AC at Q. The midpoint of BC is K and the midpoint of AC is L. Prove that the triangles RPK and RQL have the same area.
|
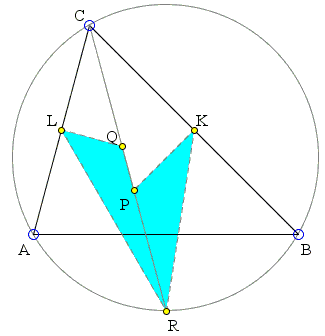
This is another solution by Bui Quang Tuan. Suppose AC ≤ BC and P, Q are reflections each of other in midpoint of CR. A line through O and perpendicular to CR intersects CR at O', AC at D, BC at E. CDRE is a rhombus with center O'. A line through Q and perpendicular to BC (RD) intersects BC at L1, RD at Q'. A line through P and perpendicular to AC (RE) intersects AC at K1, RE at P'. By symmetries of rhombus in center O',
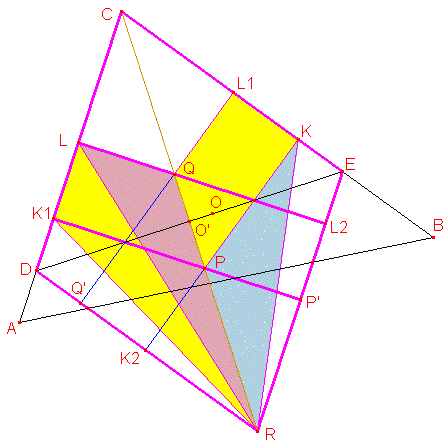
| | Area(RPK) | = Area(RQL1K) - Area(PQL1K) |
| | | = Area(RQLK1) - Area(KL1Q'K2)/2 |
| | | = Area(RQLK1) - Area (LK1P'L2)/2 |
| | | = Area(RQLK1) - Area(LK1R) |
| | | = Area(RQL). |
2007 IMO, Problem 4
|Activities|
|Contact|
|Front page|
|Contents|
|Geometry|
|Store|
Copyright © 1996-2012 Alexander Bogomolny
|
