Solution III by A. Bogomolny

Manifesto | Index | What's new | rss feed

| Bookmark |

| Follow us

| Recommend | Contact |

Triangles with Equal Area III

Here is Problem 4 from the IMO 2007:

In triangle ABC the bisector of angle BCA intersects the circumcircle again at R, the perpendicular bisector of BC at P, and the perpendicular bisector of AC at Q. The midpoint of BC is K and the midpoint of AC is L. Prove that the triangles RPK and RQL have the same area.

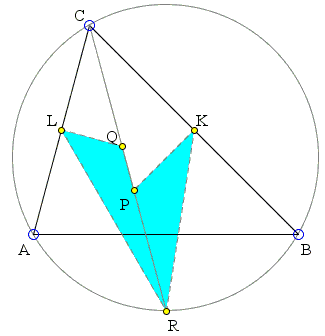
This solution makes use of some properties of similar triangles and of inscribed angles to establish the similarity.

First of all observe that Area( ΔBPR) = 2 Area( ΔRPK). This is because they share a base (PR) but the altitude of ΔBPR from B is twice that from K. Similarly, Area( ΔAQR) = 2 Area( ΔRQL). It therefore suffice to show that

(1)	Area( ΔBPR) = Area( ΔAQR).

We first show that these triangles are similar. Let angles of ΔABC be α, β γ, respectively.

Triangles ACQ and BCP are isosceles by construction. Having base angles γ/2, they are also similar. Let's record a proportion:

(2)	AC / AQ = BC / BP.

Their apex angles equal π - 2·γ/2, so that there exterior angles equal γ:

(3)	∠AQR = ∠BPR = γ.

Further

∠ARC = ∠ABC = β

so that the third angle QAR in ΔAQR equals α. Similarly, in ΔBPR,

∠BRP = α,
∠PBR = β.

It follows that triangles ABC, AQR, and BPR are similar. For their areas we have,

	Area( ΔABC) / Area( ΔAQR)	= AC² / AQ²
		= (AC / AQ)²
		= (BC/ BP)²
		= Area( ΔABC) / Area( ΔBPR).

And the required conclusion Area( ΔAQR) = Area( ΔBPR) follows.

Remark

Professor W. McWorter found a shortcut that simplifies the proof considerably. In similar triangles AQR and BPR sides AR and BR that are opposite equal angles at P and Q are equal because R is the midpoint of the arc AB implying the equality of the triangles which are then naturally have equal areas.

2007 IMO, Problem 4

40619441